Bild Nr. 3 zeigt die Elektronenmikroskopaufnahme der Bruchfläche einer Kugelschaumglasprobe aus gesintertem farbigen Altglaspulver (0≤Φ≤125μ), deren Dichte ρ=1.75gr / cm3 beträgt. Beim Sintern wurde die maximale Temperatur während 11 Minuten auf 960°C angehalten.
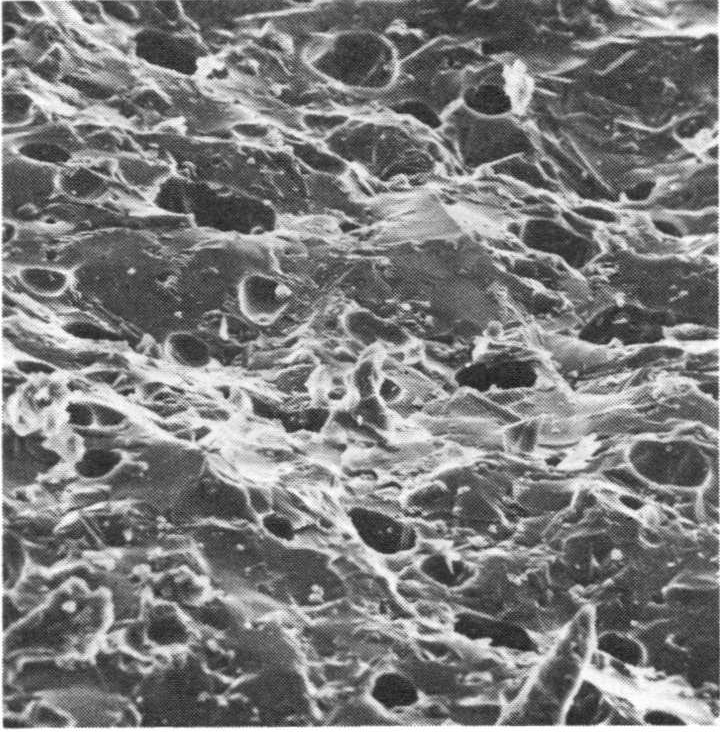
Bild Nr. 3. Bruchfläche einer Kugelschaumglasprobe im Masstab 392 : 1
Mit einer Röntgenuntersuchung konnte festgestellt werden, dass die hier behandelte Probe etwa 10 + 15 % Devitrit und Spuren von Cristobalit1) enthält. Anhand eines Dünnschliffes konnte die mittlere freie Distanz der Kugelblasen der hier dargestellten Kugelschaumglasprobe zu 80 μ bestimmt werden.
Eine Betrachtung des Anschliffes der von uns hergestellten Polyederschaumgläser zeigt im allgemeinen die in Bild Nr. 4 dargestellte Struktur.
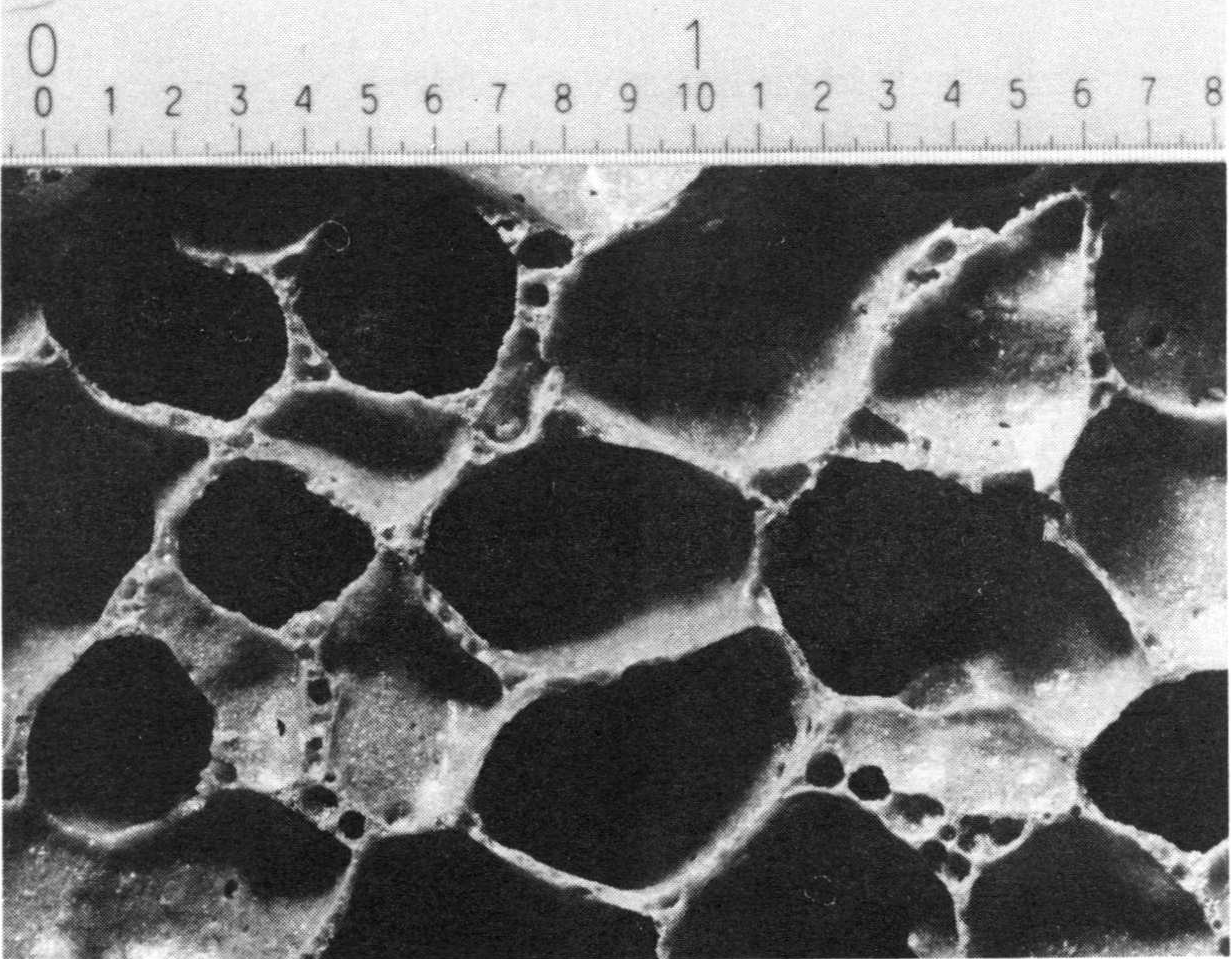
Bild Nr. 4 Anschliff einer grobzelligen Polyederschaumglasprobe
1) SiO2. ist polymorph und tritt deshalb in der Natur in drei verschiedenen Kristallformen auf:
- 1)als Quarz
- 2)als Cristobalit (kubisch) und
- 3)als Tridymit (hexagonal).
Es handelt sich hier um den Anschliff des gleichen Schaumglasquaders, wie er in Bild Nr. 1 gezeigt wurde. Man erkennt hier den Formenreichtum der unzähligen Polyederzellblasen!
Um ausdrücken zu können, dass die Zellwandungen aus formfesten und kapillarraumarmen Kugelschaumglas bestehen, wollen wir sie in Zukunft als Folien bezeichnen1).
Aufnahmen der Dünnschliffe durch eine beliebige Polyederschaumglasprobe mittels polarisiertem Licht zeigen, dass im Glas-Grundmaterial der Zellwandfolien sehr viele kleine Kristalle sowie nicht chemisch reagiertes Blähmittel eingelagert sind.
Da auch in der ursprünglichen Glasschmelze - aus der das Polyederschaumglas gebläht wird - Oberflächenspannungen wirksam sind, können die physikalischen Prinzipien für flüssige Polyederschäume, wie sie in Abschnitt 1.2 beschrieben wurden, auch auf das erstarrte Polyederschaumglas angewendet werden. Daher kann behauptet werden, dass im statistischen Mittel die Morphologie aller beliebigen zweidimensionalen Schnitte durch eine willkürliche Polyeder- schaumglasprobe durch folgende - mit den Prinzipien von J. Plateau im Einklang stehende - idealisierte Skizze ausgedrückt werden kann.
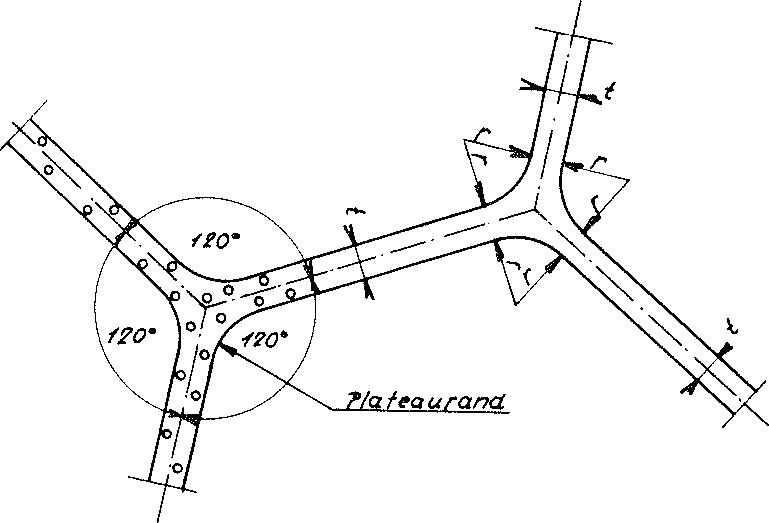
Idealisierter Schnitt durch eine Polyederschaumglasprobe
- 1) E. Manegold versteht unter einer Folie ein formfestes kapillarraumarmes Blatt, während er unter einer Membran ein formfestes kapillarraumreiches Blatt versteht (1).
Wir sehen auch, dass dort, wo drei Zellwandfolien sich normalerweise unter dem Gleichgewichtswinkel von 120° treffen, die Oberflächen mit sogenannten Plateauränder zylindrisch ausgerundet sind.