Die nun folgenden Ausführungen befassen sich mit den Aufteilungen der gesamten Gasvolumina verschiedener realer Polyederschaumgläser auf die Gasinhalte aller ihrer Polyederblasen und auf die Volumen aller Kugelporen in ihren Zellwandfolien sowie mit den stereologisch1) für jede Zelle ermittelten später definierten "Mittleren Abschnittslängen".
Wenn unter dem Porenanteil n eines Schaumglaskörpers der Dichte ρ das Verhältnis zwischen dem Gesamtvolumen aller seiner Poren und seinem Aussenvolumen verstanden wird, ergibt sich nach Ausführung einer einfachen Massenbilanz der Zusammenhang
1)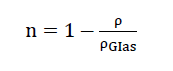
Dabei bedeutet ρGlas die Dichte des den Schaumglaskörper aufbauenden Grund-materials aus Vollglas.
Mit Hilfe einer Röntgenuntersuchung an Proben, die aus Altglaspulver mit einer für die Schaumglasblähung geeigneten Temperaturganglinie gesintert wurden, konnte festgestellt werden, dass das Grundmaterial des Schaumglases chemisch als aus normalen Gebrauchsglas bestehend angenommen werden kann. Es weist die Dichte
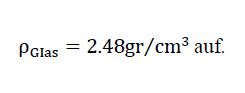
Diese Voraussetzung wurde noch durch Pyknometermessungen der Dichte der mit einer Zylindermühle aus Schaumglasprüfkörper gewonnen Grundmaterialpulver (0 ≤ ϕ ≤ 63μ) bestätigt.
Die beobachteten Werte für die Porenanteile n der von uns hergestellten Polyederschaumgläser schwanken zwischen 64 % und 90 % für das feinzellige Polyederschaumglas sowie zwischen 82 % und 90 % für die Schaumglasarten 1 und 2.
Bedeutet der Porenanteil n* das Verhältnis zwischen dem Porenvolumen in allen Zellwandfolien eines eine homogene Struktur aufweisenden Polyeder
- 1)Die Stereologie befasst sich mit dem Problem, wie mit den zweidimensionalen Beobachtungen im ebenen Schnitt auf die dreidimensionale Struktur eines Körpers geschlossen werden kann.
Schaumglaskörpers und ihrem Gesamtvolumen sowie ρ* ihre Dichte, so erhält man analog zu Gleichung Nr. 1 den Zusammenhang
2)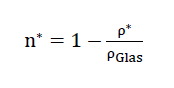
für die Zellwandfolien alleine.
Auf Grund dieser Relation war es naheliegend, die Porenanteile n* in mittelbarer Art und Weise über die Messung der Dichten ρ * der Zellwandfolien aus Kugelschaumglas zu bestimmen. Da die Dichte ρ* der Kugelschaumwandfolien unseres Wissens nur mit dem Pyknometer bestimmt werden kann, wurden die Prüfkörper - die schon einen statischen Bruchversuch erlitten - zertrümmert und diejenigen Scherben, deren Abmessungen für die Bestimmung der Dichte ρ* geeignet waren, herausgesiebt und in chemisch reinem Wasser gekocht1). Anschliessend wurden nach dem Abkühlen auf Raumtemperatur die Dichten ρ* der Zellwandfolien nach den Regeln der Pyknometermessung bestimmt.
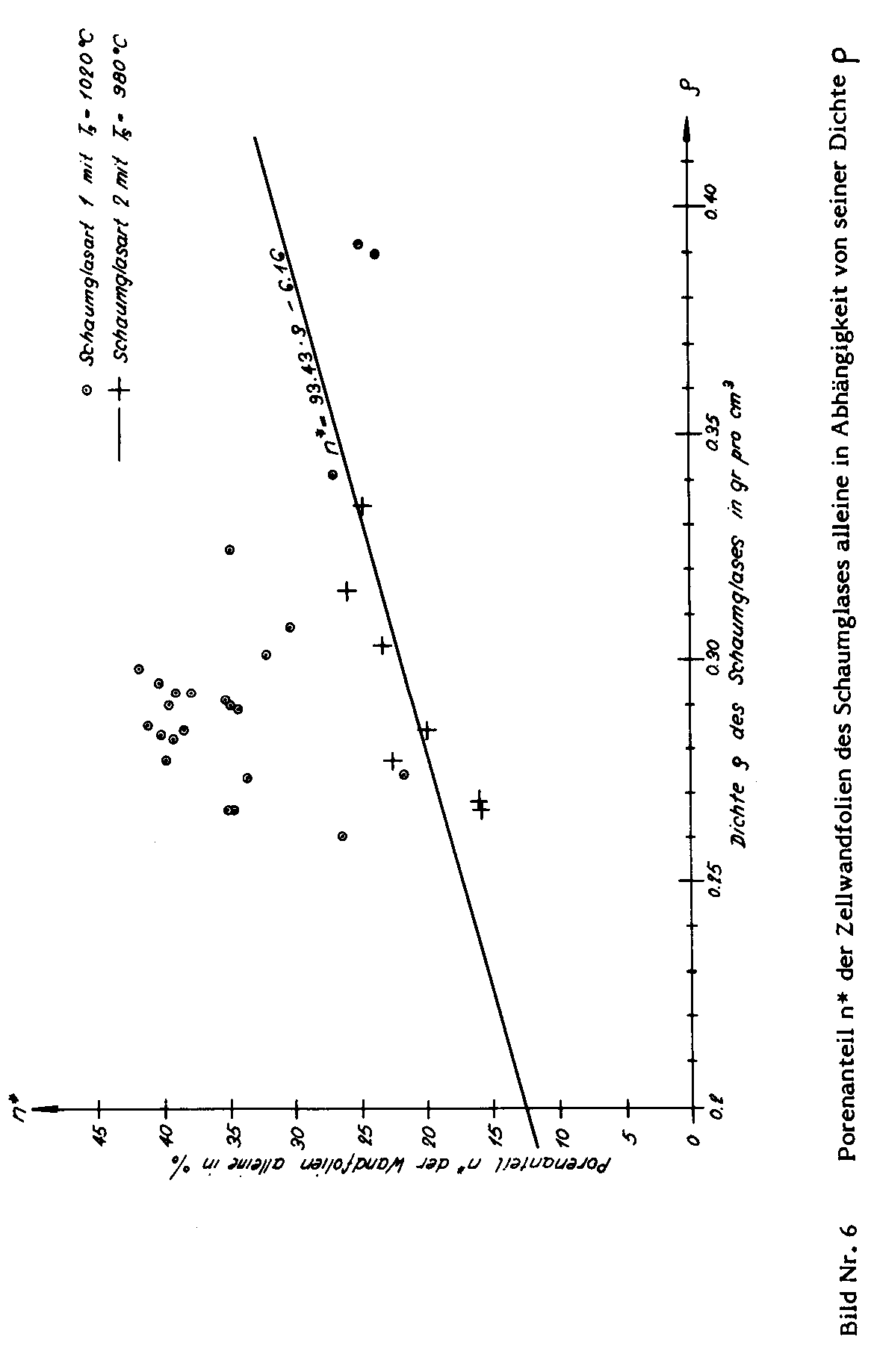
Das Diagramm auf Bild Nr. 6 zeigt Punkte, deren Koordinaten die Werte p und n* bedeuten, die an Prüfkörpern gemessen wurden, die aus den Probenreihen der Schaumglasarten 1 und 2 gewonnen wurden. Wie das Schaubild lehrt, besteht für die Proben der Schaumglasart 2, die bei verhältnismässig niedrigen Temperaturen geschäumt wurden, eine eindeutige Regression2)
3)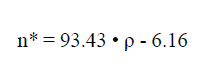
zwischen dem Porenanteil n* (%) und der Dichte ρ (gr / cm3).
Dagegen konnte bezüglich den bei verhältnismässig hohen Temperaturen geblähten Proben der Schaumglasart 1 kein solcher Zusammenhang mehr nachgewiesen werden.
- 1)Die Mischung aus Scherben und Wasser (chemisch rein) musste gekocht werden, um Gasanreicherungen an den Zellwandscherben zu vermeiden, die die Messung der Scherbendichte ρ * verfälschen würden.
- 2)Die Regression ist aber nur im Definitionsbereich 0.26 ≤ ρ ≤ 0.35gr / cm3 sichergestellt.
Wird mit nz das Verhältnis zwischen den in den Polyederblasen einer Polyederschaumglasprobe eingeschlossenen Gasvolumen und dem Probenvolumen sowie mit dem Symbol ω das Verhältnis 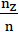 verstanden, so erhält man nach Berücksichtigung der weiter oben definierten Parameter n und n* sowie nach Ausführung einer einfachen Volumenbilanz den algebraischen Zusammenhang
verstanden, so erhält man nach Berücksichtigung der weiter oben definierten Parameter n und n* sowie nach Ausführung einer einfachen Volumenbilanz den algebraischen Zusammenhang
4)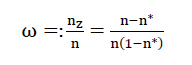
auf den später wiederholt zurückgegriffen wird.
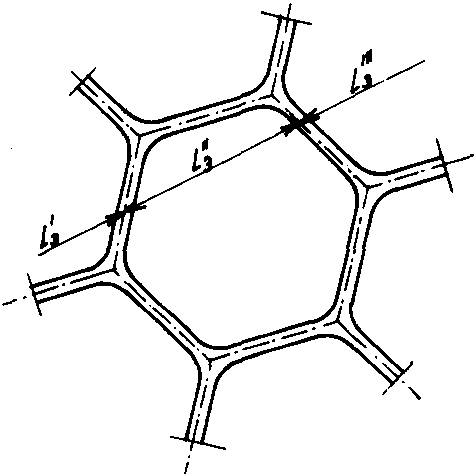
Bild Nr. 7 Definition der Mittleren Abschnittslänge L̅3
Legt man gedanklich in sämtlichen Richtungen des Raumes, der von einer beliebigen Polyederschaumglasart erfüllt ist, Geraden, so werden diese durch das aus den Elementarpolyedern gebildete Zellwerk dieses Schaumglases in unzählige ungleichlange Abschnitte 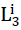 zerschnitten (siehe Bild Nr. 7). Das arithmetische Mittel dieser Teilabschnitte beträgt
zerschnitten (siehe Bild Nr. 7). Das arithmetische Mittel dieser Teilabschnitte beträgt
5)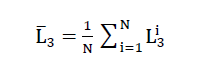
Und wird in der Stereologie als "Mittlere Abschnittslänge" bezeichnet (5). Diese Länge L̅3, die auch als "Mittlere Abschnittslänge" der raumerfüllenden Elementarpolyeder des Zellwerkes des Polyederschaumglases auf einer Testlinie gedeutet werden kann, ersetzt den landläufigen ungenauen Begriff "Zellgrösse".
Sie wurde an den in dieser Abhandlung untersuchten Polyederschaumglasproben mit Hilfe der stereologischen Gleichung
6)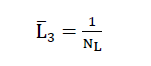
mittelbar über eine Bestimmung des Parameters NLgemessen. NLbedeutet hier die Anzahl Abschnitte der Grundpolyeder des Zellwerkes des Schaumglases pro Einheitslänge der Testlinie in einer zweidimensionalen Schnittebene (5).
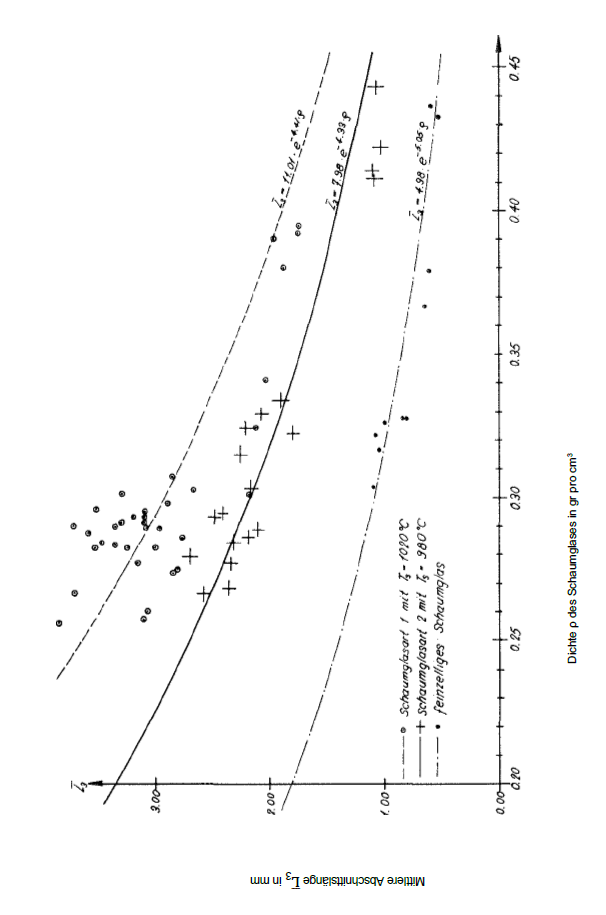
Die Koordinaten (ρ,L3) der im Diagramm auf Bild Nr. 8 eingezeichneten Punkte wurden an Proben der Schaumglasart 1 und 2 sowie des feinzeiligen Polyederschaumglases gemessen. Im gleichen Schaubild wurden auch die Kurven der aus den soeben erwähnten Messpunkten bestimmten nicht linearen Regressionsgleichungen
7)
für die Schaumglasart 1 respektive
8)
für die Schaumglasart 2 sowie
9)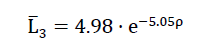
für das feinzellige Polyederschaumglas eingetragen.
Alle drei Regressionen weisen für jeden der drei behandelten Schaumglastypen einen eindeutigen Zusammenhang zwischen der Dichte ρ[gr / cm3]und der "Mittleren Abschnittslänge" L̅3 ( mm) ihrer Grundpolyeder nach. Das Diagramm zeigt auch, wie bei gleichbleibender Dichte ρ mit steigender Schäumtemperatur Ts die Abmessungen ihrer Grundpolyeder zunehmen.
Bild Nr. 8 Die Mittlere Abschnittslänge L̅3 des Schaumglases in Abhängigkeit von seiner Dichte ρ