In Abschnitt 1.1 dieses Kapitels wurde in kontinuummechanischer Betrachtungsweise ein linear-elastisches Verhalten des Glasgrundmaterials des Schaumglases bis zum Bruch angenommen. Auf Grund dieser Annahme folgt für einen beliebigen Schaumglaskörper, dessen Mikrostruktur ja vom Grundmaterial Glas aufgebaut ist, ebenfalls ein linear-elastisches äusseres Bruchverhalten. Da infolge dieser linearen Elastizität des Schaumglases ein Versagen unter beliebigen äusseren Beanspruchungsarten plötzlich unangemeldet auftritt, bezeichnet man dieses Phänomen als Sprödbruch und sagt, Schaumglas verhält sich spröde.

In Abschnitt Nr. 2 des Kapitels A wurde geschildert, wie die Dichten ρ=f (n) und die für die weiteren Betrachtungen wesentlichen Parameter n^∗ und L̅₃ der Polyederschaumgläser von der Führung des Herstellungsvorganges wesentlich abhängen. Das Gleiche gilt auch für die Zugfestigkeiten  (n^∗=0) und die Elastizitätskennwerte E(n^∗=0) und ν(n^∗=0) ihrer Glasgrundmaterialien sowie für ihre Morphologien.

Aus den soeben erwähnten Fakta und infolge der theoretisch unbegrenzten Anzahl möglicher Standardverfahren für die Schaumglaserzeugung, kann geschlossen werden, dass unzählige sich in mechanischer Hinsicht unterscheidende Schaumglastypen möglich sind. Deshalb haben wir uns auf die Prüfung der statischen Eigenschaften von grundsätzlich zwei Polyederschaumglastypen beschränkt; nämlich auf das von uns im Labor erzeugte feinzeilige Schaumglas und auf die Schaumglasarten 1 und 2. Bild Nr.

Für die experimentelle Bestimmung der Druck-, Zug- und Torsionsschubfestigkeiten sowie der Elastizitätsmoduln und Querdehnungszahlen wurde immer derselbe von uns entwickelte Standardprüfkörper verwendet, der die in Bild Nr. 49 zeichnerisch dargestellte Gestalt aufweist.

Bild Nr. 49  Standardprüfkörper

Der soeben definierte Kreiszylinder als Normform für die Herstellung der Prüfkörper aus Schaumglas stellt das Ergebnis eines Ausgleichs zwischen den beiden entgegengesetzten Forderungen nach möglichst vielen als auch nach möglichst grossen Prüflingen, die aus einer Schaumglasprobe gewonnen werden sollen, dar.

Das Verlangen nach möglichst grossen Prüfkörperabmessungen, das im Falle des Polyederschaumglases gleichwertig dem Ruf nach einer möglichst grossen integralen äusseren und inneren Oberfläche der Prüflinge gleichkommt, entspricht nach der "Statistik des spröden Bruches" von Franc A. Mc Clintock (15) der Forderung nach kleinen Standarddeviationen zwischen den einzelnen Messungen der Bruchfestigkeiten.

Die Wahl der Kreiszylinderform ermöglichte die Prüfkörper mittels eins Diamanthohlbohrers aus den Schaumglasproben bei geringem Ausschuss genau herauszuarbeiten.

Da der vorher definierte Standardprüfkörper mit den in Bild Nr. 49 festgelegten Abmessungen den Schlankheitsgrad λ=10 aufweist und aus diesem Grunde bei achsialer äusserer Druckbelastung ein einachsiger innerer Spannungszustand erreicht werden kann, wurde dieser Normkörper für die Prüfung der Druckfestigkeiten des Schaumglases verwendet.

Bild Nr. 50 zeigt einen noch unbelasteten Prüfkörper aus Polyederschaumglas in der Belastungsvorrichtung der von uns verwendeten Prüfmaschine. Die im Bild ersichtlichen, an den beiden Lagerflächen des Prüflings angeordneten 3 mm dicken Kunstgummiplatten verhindern seine vorzeitige Zerstörung durch ungleichmässige örtliche Pressung.

Zur Ueberprüfung der Richtigkeit dieses Vorgehens wurden auch Druckversuche bei Variation der Stärke der Lagerplatten aus Neoprengummi ausgeführt. Dabei konnte festgestellt werden, dass Aenderungen der Gummilagerplattendicken keinen wesentlichen Einfluss auf die Ergebnisse der Druckfestigkeiten ausüben. Besonders schlecht schnitten dabei die Prüflinge ab, die nicht mit Gummilagerplatten versehen wurden.

Bild Nr. 50Prüfkörper aus Polyederschaumglas in der Belastungsvorrichtung für den Druckversuch

Bei der Prüfung der Druckfestigkeiten σ_dB des Schaumglases beginnt der Versuch immer mit einem in Abhängigkeit von den Dehnungen ε linearem Ansteigen der Druckspannungen σ im Prüfkörper bis zum plötzlichen unangemeldeten Bruch bei σ_dB, der sich im dazugehörenden und in Bild Nr. 51 dargestellten Spannungs - Dehnungsdiagramm mit einem gleichzeitigen schroffen Abfallen der Druckbeanspruchung bemerkbar macht. Bild Nr.

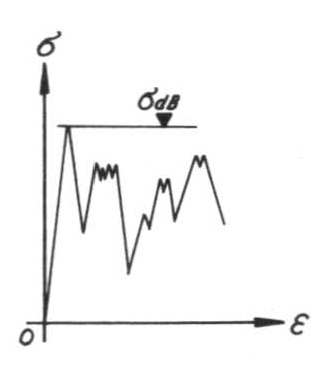
Bild Nr. 51Spannungs - Dehnungsdiagramm beim Druckversuch

Wird anschliessend der Versuchsablauf ohne Unterbruch fortgesetzt, so wird der Prüfling unter ständigem Knistern zerpulvert, wobei die aufgebrachten Druckspannungen ständig um einen auf tieferem Niveau als die Druckfestigkeit σ_dB liegenden Mittelwert pendeln.

Mit Druckversuchen an Prüflingen verschiedener Geometrie konnte festgestellt werden, dass ihre Gestalt und Grösse einen nicht unerheblichen Einfluss auf ihre Druckfestigkeiten ausüben! Deshalb sollen die so erhaltenen Druckfestigkeiten nur als Vergleichs werte betrachtet werden. Während dem Prüfvorgang betrug die Geschwindigkeit des Zusammenfahrens der in Bild Nr. 50 ersichtlichen Stahlauflagerteller 1,2 mm pro Minute.

Besondere Würdigung verdient noch die Erkenntnis, wie das bei jedem Druckversuch beobachtete lineare Spannungs - Dehnungsverhalten bis zum Bruch die theoretisch vorausgesagte Gültigkeit der linear-elastischen Bruchmechanik für das Schaumglas im Rahmen der Messgenauigkeit bestätigt.

Tabelle Nr. 1 enthält die mit der eben beschriebenen Prüfmethode bestimmten Druckfestigkeiten des feinzeiligen Polyederschaumglases. Aus Sechzehn der in ihr eingetragenen zusammengehörenden Wertepaare aus Dichte und Druckfestigkeit, die einer nicht linearen Regressionsanalyse unterwofen wurden, enthält man für das feinzellige Polyederschaumglas die Regression

87)σ_dB=16.24⋅ρ^1,57+1.10

die die Druckfestigkeit σ_dB (N / mm²) mit der Dichte ρ (gr / cm³) in Beziehung bringt und deren Graphen im Diagramm auf Bild Nr. 26 eingetragen wurde. Die Regression ist aber nur im Bereiche 0.29 < ρ < 0.52gr / cm³ sichergestellt.

Die Tabellen Nr. 2 und Nr. 3 enthalten die mit unserer Standardmethode beobachteten Druckfestigkeiten der Schaumglasarten 1 und 2. Die Prüfergebnisse für die Probenreihe der Schaumglasart 1 können durch die Regressionsgleichung

88)σ_dB=10.96⋅ρ^1,07⋅e^{(0,0042 n∗-0.336 L̅₃)}+0.22

zusammengefasst werden. Dabei bedeutet σ_dB (N/mm²) die Druckfestigkeiten, ρ (gr/cm³) die Dichte, n^∗(0/0) der Porenanteil der Zellwandfolien und L̅₃(mm) die "Mittleren Abschnittslängen" der Schaumglasart 1. Die Regression ist in den Intervallen

• 0.26 ≤  ρ≤ 0.39gr / cm³,
• 21 ≤ n^∗ ≤ 4 2% und
• 1.9 ≤ L̅₃ ≤ 3.8 mm

für die unabhängigen Argumente sichergestellt.

Analog gilt für die Probenreihe der Schaumglasart 2 die Gleichung

89)σ_dB=20.43⋅ρ^2.89⋅𝚎^{(0.021 n∗-0.00016 L₃)}+0.74

Dabei gilt:

• 0.26 ≤ ρ ≤ 0.34gr / cm³ ,
• 15 ≤ n^∗ ≤ 26%  und
• 1.9 ≤ L̅₃ ≤ 2.6mm.

Im Diagramm auf Bild Nr. 26 wurden auch die Punkte eingetragen, die zu den Prüfkörper gehören, deren gemessene Parameter σ_dB,ρ,n^∗ und L̅₃ in die zu den Gleichungen Nr. 88 und Nr. 89 führenden Regressionsanalysen einbezogen wurden.

Wie in Abschnitt Nr. 2 des Kapitels A ausgeführt wurde, bestehen für die feinzelligen Polyederschaumgläser und die Proben der Schaumglasarten 2 - die alle bei verhältnismässig niedrigen Temperaturen geschäumt wurden - eindeutige Regression zwischen der Dichte ρ und den Parametern n^∗ und L̅₃. Dies trifft aber für die Werte n^∗ der mit relativ hohen Temperaturganglinien geblähten Proben der Schaumglasart 1 nicht mehr zu.

Auf der Grundlage dieser Beobachtungen kann die Hypothese aufgestellt werden, dass die Struktur (n^∗=n^∗(ρ),L̅₃=L̅₃(ρ)) und somit auch das mechanische Verhalten von beliebigen bei relativ niedrigen Temperaturen geblähten Polyederschaumglastypen im wesentlichen nur von ihrer Dichte ρ abhängt, während dies in Bezug auf die mit relativ hochtemperaturigen Ganglinien geblähten Typen nicht mehr gilt (n^∗≠n^∗(ρ),L̅₃=L̅₃(ρ)).

Mit obenstehenden Ausführungen über die empirisch gewonnenen Zusammenhänge zwischen den Parametern n^∗ und L₃ von Proben verschiedener Polyederschaumglasarten und ihrer Dichte ρ sowie der mit Hilfe eines Vergleiches der Regressionsgleichungen Nr. 87, 88 und 89 festgestellten allgemeinen Abhängigkeit

90)σ_dB=f (ρ,n^∗,L̅₃)

kann obige Hypothese bestätigt werden.

Bild Nr. 52

Die kreiszylindrische Gestalt der bereits früher für alle statischen Versuchsarten normierten Prüfkörper aus Schaumglas legt es nahe, ihren Widerstand gegen reine Torsionsbeanspruchung zu prüfen. Ein auf den Schaumglasprüfzylinder wirkendes äusseres achsiales Torsionsmoment Mt (siehe Bild Nr. 52) verursacht in seinem kreisförmigen Querschnitt Schubspannungen τ(r), die nach den Lehren der Mechanik gemäss der bekannten Beziehung

91)

linear mit dem Schwerpunktabstand r vom Wert 0 im Querschnittsschwerpunkt bis zum grössten Wert

92)

am Umfang des Querschnitts (r=R) zunehmen. Dabei beträgt das polare Trägheitsmoment der Kreisquerschnittfläche

Bild Nr. 53 Versuchsaufbau bei der Bestimmung der Torsionsschubfestigkeit

In der auf Bild Nr. 53 dargestellten Prüfeinrichtung werden die Torsionsmomente Mt über rotationssymmetrische Stahlwiderlager auf die Schaumglaszylinder übertragen. Diese Widerlager wurden vor dem Einbau in die Versuchseinrichtung unter Benutzung einer Lehre an die Endflächen der Schaumglasprüfkörper geklebt.

Während dem Versuch kann ein lineares Ansteigen des Drehmomentes in Abhängigkeit vom Verdrehwinkel bis zum Betrage MtB im Augenblick des plötzlichen Bruches beobachtet werden. Dabei betrug bei jedem Torsionsversuch die Geschwindigkeit der gegenseitigen Verdrehung der Prüfzylinderenden 0.20 Grade pro Minute. Die Randspannungen erreichen im Moment des Versagens des Prüflings die Torsionsschubfestigkeit

93)

mit

Bild Nr. 54 Das typische Bruchbild beim Torsionsversuch.

Bild Nr. 54 zeigt die sich bei jedem Versuch ohne Voranmeldung plötzlich ausbildende typische Torsionsbruchfläche.

Tabelle Nr. 1 enthält die mit der eben beschriebenen Prüfmethode bestimmten Torsionsschubfestigkeiten des feinzelligen Polyederschaumglases. Aus fünf der in ihr eingetragenen zusammengehörenden Wertepaare aus Dichte und Torsionsschubfestigkeit erhält man die nicht lineare Regression

94)τ_B=20.70⋅ρ^3.12+0.21

welche die Torsionsschubfestigkeit τ_B(N / mm²) des feinzeiligen PolyederSchaumglases mit seiner Dichte ρ(gr / cm³) in Beziehung bringt und deren Graphen im Diagramm auf Bild Nr. 31 eingetragen wurden.

Bild Nr. 55 Aufbau des Zugversuches

Bild Nr. 56

Die Bilder Nr. 55 und Nr. 56 zeigen die Fotographien der Versuchseinrichtung, die für die Prüfung der reinen Zugfestigkeit des Schaumglases im Zugversuch aufgebaut wurde. Auf die beiden Endflächen der Prüfkörper (Standardprüfkörper) wurden mittels Epoxidharz zwei kreiszylindrische Stahlkappen geklebt. Diese ermöglichen ein einwandfreies Einleiten der äusseren achsialen Zugkräfte in die Prüfkörper. Um während dem Versuchsablauf möglichst genaue einachsige Normalspannungszustände zu erreichen, wurden auf die beiden Seiten der Prüfkörper Kugelgelenke angeordnet.

Beim Prüfen kann ein lineares Ansteigen der aufgebrachten äusseren Zugkraft in Abhängigkeit von der Dehnung ε bis zum Betrage NB im Moment des plötzlichen Bruches beobachtet werden. Dabei betrug bei jedem Zugversuch die Geschwindigkeit der Verlängerung der Prüfzylinderachse 0.12 mm pro Minute. Die Normalspannungen erreichen beim Versagen des Prüflings die Zugfestigkeit

95)

F₀ bedeutet die Querschnittsfläche des Prüfkörpers.

Wie Bild Nr. 57 zeigt, erfolgt der Bruch i.a. in nächster Nähe einer Klebestelle. Diese Erscheinung kann durch den mehrachsigen Spannungszustand in der näheren Umgebung der Klebefuge erklärt werden.

Bild Nr. 57Das Bruchbild beim Zugversuch

Tabelle Nr. 1 enthält die mit der eben beschriebenen Prüfmethode bestimmten Zugfestigkeiten des feinzeiligen Polyederschaumglases. Aus den sieben in ihr eingetragenen zusammengehörenden Wertepaare aus Dichte und Zugfestigkeit erhält man die nicht lineare Regression

96)σ_B=3.53⋅ρ^1,44+0.01

welche die Zugfestigkeit σ_B(N / mm²) des feinzelligen Polyederschaumglases mit seiner Dichte ρ(gr / cm³) in Beziehung bringt und deren Graphen im Diagramm auf Bild Nr. 27 eingetragen wurden.

Da die Zugfestigkeiten σ_B der Polyederschaumgläser bei gleichbleibender Dichte ρ viel kleinere Werte annehmen als die zugehörigen Druckfestigkeiten σ_dB, können ihre statischen Elastizitätsmoduln E nur im Druckversuch bestimmt werden.

Die Skizze auf Bild Nr. 58 und Bild Nr. 59 zeigen die Ansicht der von uns entwickelten Prüfeinrichtung.

Bild Nr. 58  Aufbau der Messvorrichtung für die Bestimmung des Elastizitätsmoduls des Schaumglases

Um eine möglichst eindeutige Normalkrafteinleitung in die Schaumglasprüfzylinder zu gewährleisten, wurde die symmetrische Messvorrichtung mittels zweier Kugeln im Druckrahmen der Zwickmaschine aufgelagert.

Symmetrisch zur Vertikalaxe der ganzen Versuchsvorrichtung wurden zwei Induktive Verlagerungsgeber des Typs PR 9310 der Firma Philips befestigt, um die Verkürzung der Prüfkörperaxe durch messen und ausmitteln der Vertikalverschiebungen der beiden links und rechts angeordneten Stahlscheiben in Funktion der Belastung P zu bestimmen.

Die Prüfzylinder weisen alle die bereits früher auf Bild Nr. 49 festgelegten Standardabmessungen auf.

Bild Nr. 59

Bild Nr. 60 zeigt das Blockschema der elektronischen Messeinrichtung, die die Signale der beiden Induktiven Verlagerungsgeber addiert.

Eine Eichung ergab, dass die Einheitslänge 1 cm auf dem x-y-Schreiber in Richtung der Abszisse 3.11μ Verkürzung der Prüfkörperaxe bedeutet und in Richtung der Ordinate y 61.50 N Normalkraftaufbringung gleichkommt.

Bild Nr. 60

Vor jeder Elastizitätsmodulmessung wurde mit der Zwickmaschine eine Vorbelastung von 200 N auf den Prüfkörper aufgebracht.

Die Geschwindigkeit der Verkürzung der Prüfzylinderachse betrug immer  mm / Min.

Während dem Messvorgang trägt der x-y-Schreiber selbsttätig für jeden Lastzyklus den Graphen P=f (/ΔL/) auf, der i.a. folgenden schematischen Verlauf zeigt:

Wenn unter L_o und F_o die Länge beziehungsweise der Querschnitt des unbelasteten Prüfkörpers aus Schaumglas verstanden wird, betragen im Schaumglas unter der Belastung P die Normalspannungen

97)

und die dazugehörenden Längsdehnungen

98)

Schlussendlich erhält man per definitionem den Elastizitätsmodul zu

99)

Für jeden Prüfkörper wurden die Elastizitätsmoduln zweimal bestimmt (beim zweiten Mal wurde der Prüfling um 90° im Uhrzeigersinn um seine Längsachse gedreht) und dann das erhaltene Wertpaar für E ausgemittelt.

Die Tabellen Nr. 1 bis und mit Nr. 3 enthalten die Resultate der nach der soeben beschriebenen Methodik ausgeführten Messungen der Elastizitätsmoduln des feinzeiligen Polyederschaumglases sowie der Schaumglasarten 1 und 2.

Im Diagramm auf Bild Nr. 33 wurden die Punkte eingetragen, deren Koordinaten die gemessenen Werte ρ und E bedeuten.

Auf Grund seiner niedrigen Zugfestigkeiten können die Querdehnungszahlen des Schaumglases nur im Druckversuch geprüft werden. Deshalb brauchte die für die Messung der Elastizitätsmoduln E benutzte Versuchseinrichtung nur geringfügig abgeändert zu werden. Die Skizze auf Bild Nr. 61 zeigt die Ansicht der Aufbaues.

Die Prüfkörper weisen alle die bereits früher auf Bild Nr. 49 festgelegten Standardabmessungen auf. Auf die Grund- und Deckflächen aller Prüfzylinder wurden mit Hilfe einer Lehre 10 mm dicke Stahlscheiben mittels Epoxidharz geklebt.

Zur Bestimmung der Querdehnungszahl ν des Schaumglases im Druckversuch muss die Verkürzung der Längsachse des Prüfzylinders und die gleichzeitig auftretende Verlängerung seiner Durchmesser in Abhängigkeit von der Belastung P gemessen werden. Darum wurden die beiden Induktiven Verlagerungsgeber symmetrisch zur Zylinderachse angeordnet, und zwar so, dass ihre Achsen auf der Verlängerung eines Durchmessers durch den Prüfkörperschwerpunkt liegen.

Bild Nr. 61Aufbau der Messvorrichtung für die Bestimmung der Querdehnung ν des Schaumglases

Da nach der Verlängerung ΔD eines durch den Schwerpunkt des Prüfkörpers gehenden Durchmessers gefragt wird, müssen die Signale der beiden Induktiven Verlagerungsgeber addiert werden. Somit konnte die für die Elastizitätsmodulmessung benutzte elektronische Messvorrichtung (siehe Blockschema auf Bild Nr. 60) wiederverwendet werden.

Eine Eichung ergab, dass die Einheitslänge 1 cm auf dem x-y-Schreiber in Richtung der Abszissenachse x 1,22μ Verlängerung des Prüfzylinderdurchmessers bedeutet und in Richtung der Ordinate y 61,47 N Normalkraftaufbringung gleichkommt.

Vor der eigentlichen Messung wurde jeder Prüfkörper mit einer Kraft von 200 N vorbelastet. Die Geschwindigkeit der Verkürzung der Prüfzylinderachse betrug immer  mm pro Minute. Während dem Messvorgang trägt der x-y-Schreiber selbsttätig für jeden Lastzyklus den Graphen P=f (ΔD) auf, der i.a. folgenden schematischen Verlauf zeigt:

Wenn unter D_o und F_o der Durchmesser beziehungsweise der Querschnitt der unbelasteten Schaumglasprobe verstanden wird, betragen im Schaumglas unter der Last P die Normalspannungen

100)

und die dazugehörenden Querdehnungen

101)

Mit dieser Messeinrichtung kann aber die gleichzeitige Längsdehnung ε_I der Prüfzylinderachse nicht gemessen werden. Deshalb wurden die für die Elastizitätsmodulmessung benutzten Prüfkörper wiederverwendet, um die zu P und ε_q=ε_q(P) gehörenden Längsdehnung ε_I der Prüfkörperachse mit Hilfe des gemessenen E-Moduls aus der Beziehung

102)

rechnerisch zu erhalten.

Schlussendlich erhält man per definitionem die Querdehnungszahl des Schaumglases zu

103)

Die Tabellen Nr. 1 bis und mit Nr. 3 enthalten die Resultate der nach der

soeben beschriebenen Methodik ausgeführten Messungen der Querdehnungszahlen ν des feinzelligen Schaumglases sowie der Schaumglasarten 1 und 2. Im Diagramm auf Bild Nr. 34 wurden die Punkte eingetragen, deren Koordinaten die gemessenen Werte ρ und ν bedeuten.