Wie die Ausführungen in Kapitel A dieser Abhandlung zeigen, enthalten die Zellwandfolien der realen Polyederschaumgläser sehr viele Poreneinschlüsse und können damit als Kugelschaumglas idealisiert werden. Beispielsweise schwanken die Porenanteile n* der Zellwandfolien bei den Schaumglasarten 1 und 2 zwischen 16 % und 42 %. Es wurde auch gezeigt, dass das Grundmaterial der Zellwandfolien dem kompakten Gebrauchsglas entspricht, dessen Dichte zu ρGlas=2.48 angenommen werden kann.
Aufgrund der soeben erwähnten Fakten und im Hinblick auf das Ziel, den Rechenaufwand für die Voraussage der mechanischen Eigenschaften des Polyederschaumglases mittels eines Computers in einem vernünftigen Rahmen zu halten, werden in Zukunft seine aus Kugelschaumglas bestehenden Zellwandfolien als Kontinuum aufgefasst, das folgende mechanische Eigenschaften aufweisen soll:
- 1)
Die einachsige Zugfestigkeit des Kontinuums betrage im ebenen Spannungszustand
20)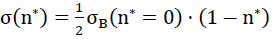
- 2)
Sein Elastizitätsmodul habe den Wert
21)E(n∗)=E(n∗=0)e−3.95n∗
- 3)
Die Querdehnungszahl des Kontinuums sei
22)ν(n∗)=ν(n∗=0)=0.21
In den obigen Formeln Nr. 20 bis und mit Nr. 22 werden im Blick auf die spätere Verwendung die bruchmechanischen und elastischen Kennwerte des Grundmaterials der als Kontinuum behandelten Kugelschaumglasfolien zu
- σGM(n∗=0)=90N / mm2
- E(n∗=0)=72´600N / mm2 und
- ν(n∗=0)=0.21 angenommen
Diese Werte entsprechen einer Glasart, die i.a. die folgende chemische Zusammensetzung in Gewichtsprozenten aufweist:
73 % SiO2, 15 % Na2O, 10 % CaO, 1 % Al2O3 und 0,05 % Fe2O3.
Die in Abschnitt Nr. 2 dieses Kapitels experimentell bestimmten mechanischen Materialkennwerte wurden an Prüfkörpern gemessen, die aus Proben herausgearbeitet wurden, die aus Altglaspulver von ungefähr obiger chemischer Zusammensetzung geschäumt wurden. Daher scheinen obige Annahmen für das Grundmaterial der Kugelschaumglasfolien des Polyederschaumglases bezüglich eines späteren Vergleiches der theoretisch vorausgesagten und experimentell bestimmten Bruchfestigkeiten, Elastizitätsmoduln und Querdehnungszahlen vernünftig und sinnvoll.
Weiter wird für die künftige Ermittlung der Bruchfestigkeiten des Polyederschaumglases die Hypothese auf gestellt, wonach der Bruch im Polyederschaumglas auf der Oberfläche derjenigen Zellwandfolie aus Kugelschaumglas mit dem Porenanteil n* beginne, wo die grösste überhaupt im Schaumglas auftretende oberflächliche Hauptzugspannung gerade die Zugfestigkeit
16a)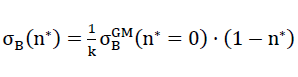
der betreffenden als Kontinuum aufgefassten Wandfolie erreicht.
Da als Folge der Hypothese in Abschnitt Nr. 1.3.1 dieses Kapitels die initialen Zerstörungen des Polyederschaumglases infolge beliebigen äusseren Beanspruchungen auf den Oberflächen der als Kontinuum aufgefassten Zellwandfolien aus Kugelschaumglas beginnen, sollen die Spannungszustände auf diesen Flächen möglichst gut bekannt sein!
Um diese Beanspruchungszustände im Rahmen eines vernünftigen Aufwandes numerisch zu bestimmen, wurde daher von dem in Abschnitt Nr. 1.4.1 des Kapitels A erwähnten Idealschaumglas ausgegangen, bei dem die Mittelflächen der Zellwandfolien ein Zellwerk bilden, das aus lauter kongruenten Kelvin'schen Elementarpolyedern (auch α - Tetrakaidekahedron genannt) besteht. Dabei wurden nun aber alle doppeltgekrümmten sechseckigen Seitenflächen seiner Grundpolyeder zu ebenen Flächen deformiert. Durch diese Operation ergibt sich ein neues Polyederschaumglasmodell, das auf den Bildern Nr. 11 und Nr. 12 dargestellt wurde. Die Elementarpolyeder des Zellwerkes des neuen Polyederschaumglasmodells bestehen nun aus lauter kongruenten Abgeschnittenen Oktaedern (einer der dreizehn Archimedischen Körper). Ihre Gestalt wurde auf Bild Nr. 13 festgehalten. Aus diesem Grunde wollen wir das soeben gefundene Modellpolyederschaumglas Modellschaumglas "TOP" nennen 1).
Zwar sind im Modellschaumglas "TOP" die in den Bedingungen a) und b) von J. Plateau (siehe Abschnitt 1.2 des Kapitels A) angegebenen Winkel nicht mehr eingehalten! Da sich diese Abweichungen nur in den näheren Umgebungen der "Kanten" der Kelvinpolyeder bemerkbar machen, können sie vernachlässigt werden. Die Morphologie der einzelnen Abgeschnittenen Oktaeder, die als Elementarpolyeder das Modellschaumglas "TOP" aufbauen, kann durch die Symmetrie einer der 32 Kristallklassen (Punktgruppen) der Kristallographie beschrieben werden (11).
- 1)"TOP" = Abkürzung für "Truncated Octahedron Plateau". "Truncated Octahedron" ist das englische Wort für Abgeschnittener Oktaeder.
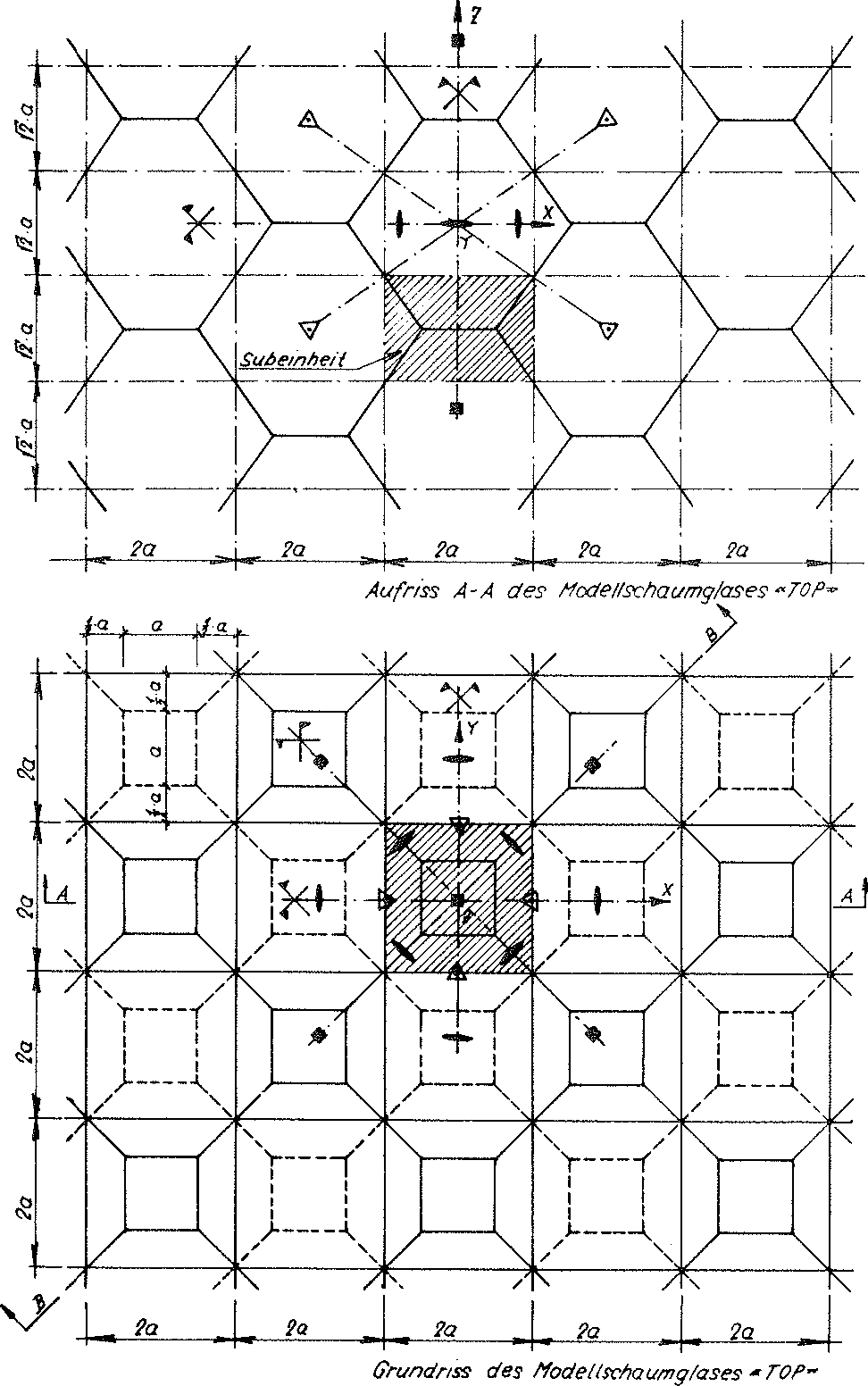
Bild Nr. 11 Grund- und Aufriss des Modellschaumglases "TOP"
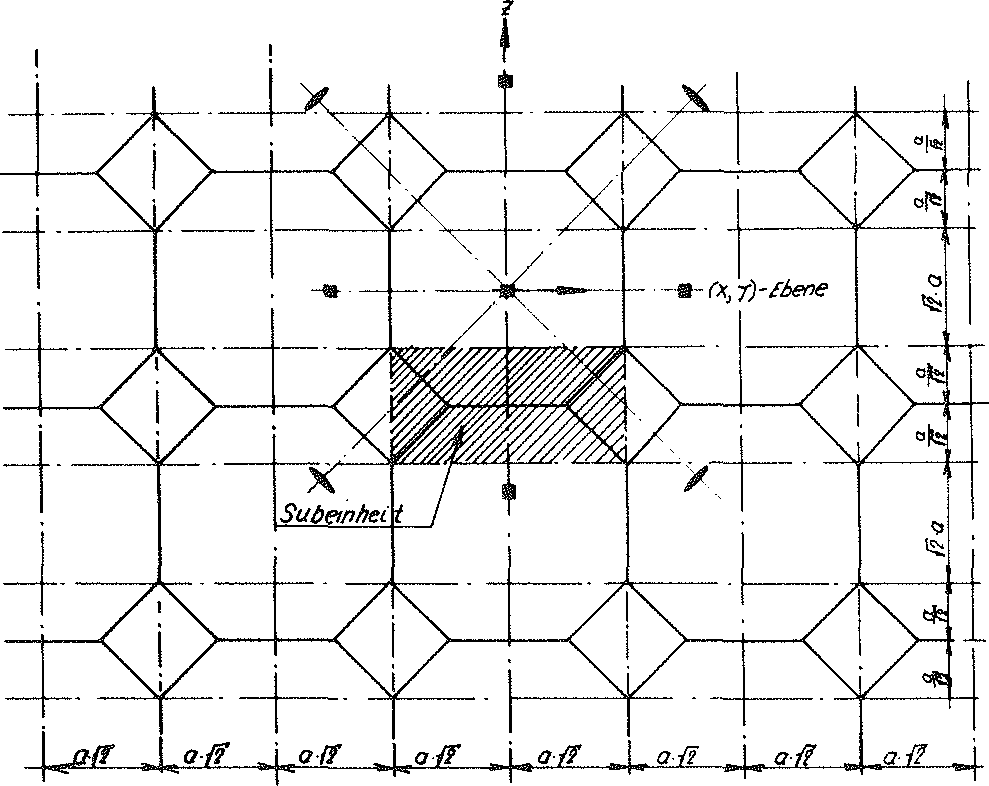
Bild Nr. 12 Schnitt B-B des Modellschaumglases "TOP"
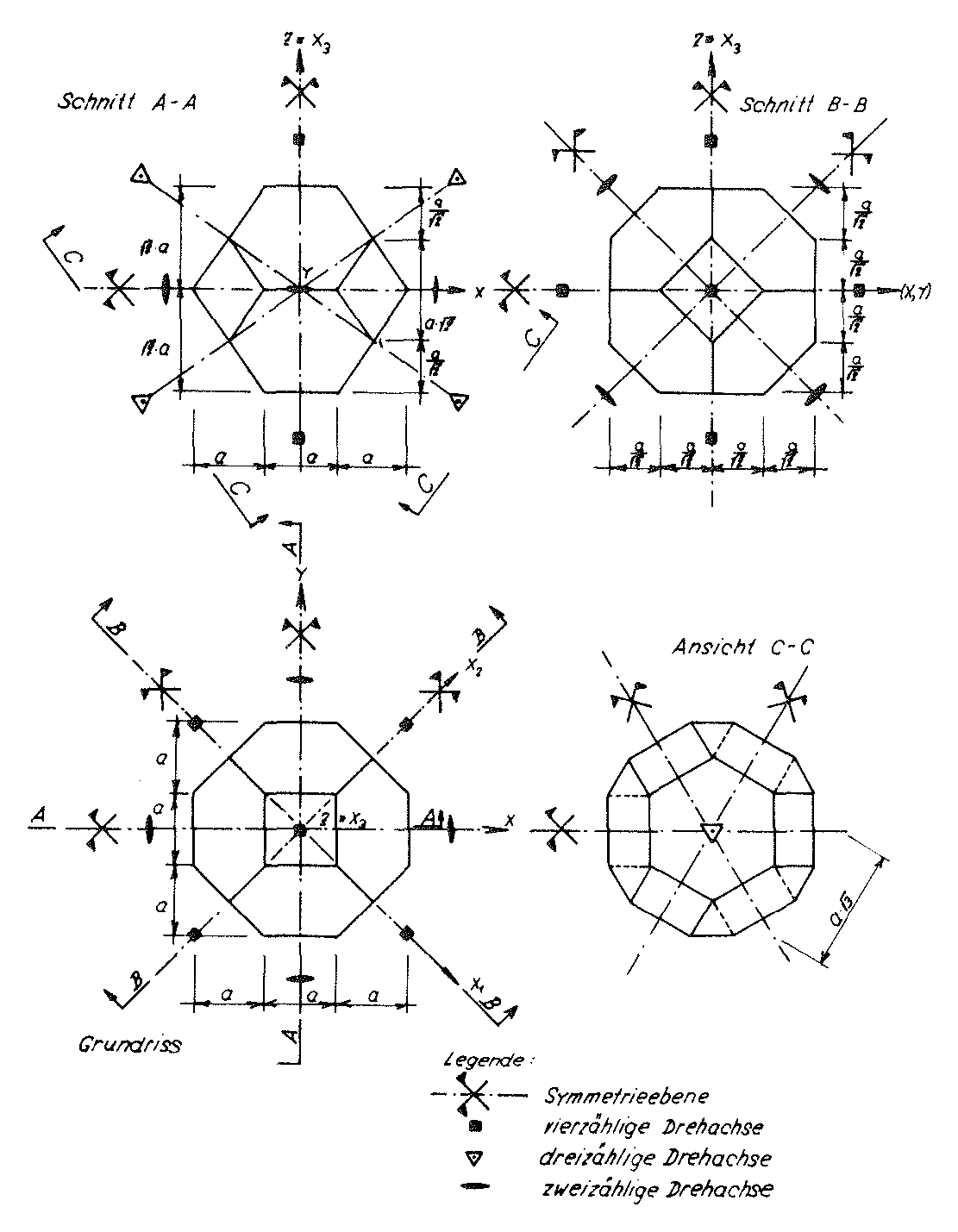
Bild Nr. 13 Das Abgeschnittene Oktaeder als Elementarpolyeder des Modellschaumglases "TOP"
Mit Hilfe des Bildes Nr. 13 können die Symmetrieelemente der Punktgruppe dieser Abgeschnittenen Oktaeder auf folgende Weise beschrieben werden:
- 1)Das Abgeschnittene Oktaeder besitzt drei vierzählige Drehachsen 1), die paarweise normal aufeinanderstehen und je durch die Schwerpunkte seiner gegenüberliegenden Quadratseitenflächen bestimmt werden;
- 2)Das Polyeder weist aber auch vier dreizählige Drehachsen auf, deren Lagen je durch die Schwerpunkte seiner gegenüberliegenden Sechseckseitenflächen festgelegt werden;
- 3)Das Elementarpolyeder weist dazu sechs zweizählige Drehachsen auf, die je durch die Mittelpunkte gegenüberliegender Schnittkanten je zweier seiner Sechseckseitenflächen bestimmt werden;
- 4)Das Grundpolyeder hat auch neun Symmetrieebenen, die auf seinen zwei- oder vierzähligen Drehachsen je senkrecht stehen und immer seinen Schwerpunkt enthalten; und
- 5)Ein Symmetriezentrum im Schwerpunkt des Polyeders.
Die soeben aufgezählten Symmetrieelemente bilden eine Punktgruppe oder Kristallklasse, die i.a. mit dem international gebräuchlichen Symbol m 3 m bezeichnet und zum kubischen Kristallsystem zugeordnet wird. Da das Hexakisoktaeder als allgemeine Form auch zu dieser Kristallklasse gehört, kann man diese Klasse oder Punktgruppe mit dem Synonym "Hexakisoktaedrische Klasse" bezeichnen.
Die Beschreibung des Modellschaumglases "TOP" mit den Bildern Nr. 11 bis und mit Nr. 13 zeigt, dass infolge des periodischen Aufbaues seines Zellwerkes alle für seine einzelnen herausgelösten Grundpolyeder soeben beschriebenen Symmetrieelemente auch auf das gesamte allseitig unbegrenzte Modellschaumglas "TOP" übertragen werden können. Man kann daher sagen, dass das Zellwerk des Modellschaumglases "TOP" auch zur Kristallklasse oder Punktgruppe m 3 m gehört.
In Abschnitt Nr. 1.3.2 des Kapitels A wurde am Beispiel des realen Polyederschaumglases gezeigt (siehe auch Bild Nr. 14), dass dort, wo drei Zellwandfolien sich normalerweise unter dem Gleichgewichtswinkel von 120° treffen, die
- 1)Kommt ein Körper nach Drehung mit dem Winkel α =
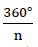 um eine mit dem Körper festverbundene Gerade mit sich selbst zur Deckung, so nennt man diese eine "n - zählige Drehachse".
um eine mit dem Körper festverbundene Gerade mit sich selbst zur Deckung, so nennt man diese eine "n - zählige Drehachse".
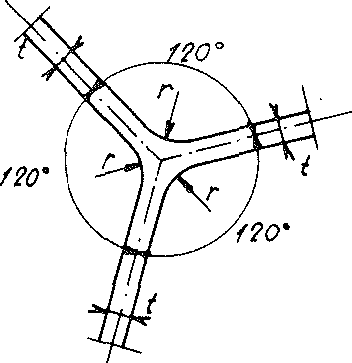
Bild Nr. 14 Der Schnittbereich dreier Zellwandfolien
Oberflächen mit sogenannten Plateauränder zylindrisch ausgerundet sind, im gleichen Abschnitt wurde auch festgestellt, dass im realen Polyederschaumglas die Zellwandfolien als aus Kugelschaumglas bestehend angenommen werden können. Aus diesem Grunde werden von jetzt an diese beiden Fakta mitberücksichtigt.
Für das Modellschaumglas "TOP" besteht ein einfacher Zusammenhang zwischen der Geometrie des Modells und dem Porenanteil nz=n⋅ω , der von allen Zellwandfolien aus Kugelschaumglas eingeschlossen wird.
Auf Bild Nr. 13 dieses Abschnittes wurde ein Elementarpolyeder unseres Modellschaumglases "TOP" dargestellt, dessen Zellwandmittelflächen ein Zellwerk bilden, das aus lauter solcher kongruenter "Abgeschnittener Oktaeder" aufgebaut ist. Bild Nr. 15 zeigt den Schnitt dieses Grundpolyeders und seiner Abschlusspartien mit der (y - z) oder (x - z) - Ebene.
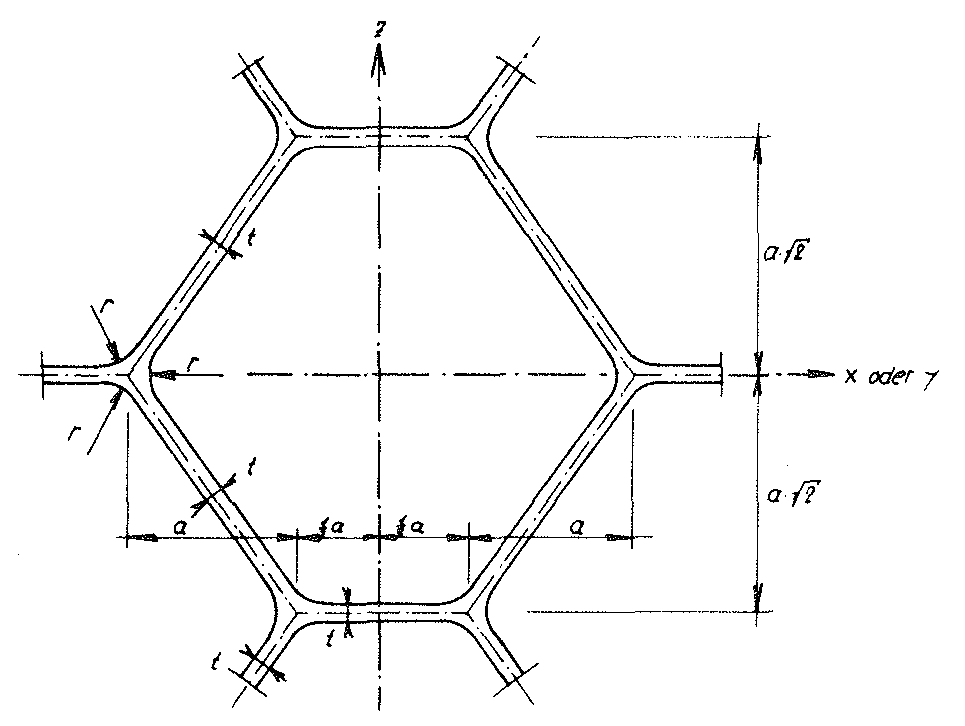
Bild Nr. 15 Schnitt des Grundpolyeders des Modellschaumglases "TOP" mit der xz- oder yz - Ebene
Die auf die Volumeneinheit bezogene Mittelfläche der Wandfolien aus Kugelschaumglas des Modellschaumglases "TOP" beträgt
23)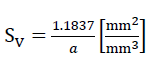
Dabei bedeutet a die Kantenlänge der Grundpolyeder des Zellwerkes, das die Mittelflächen der Zellwandfolien des Modellschaumglases bilden.
Unter Vernachlässigung der in Bild Nr. 15 eingezeichneten Plateauränder mit dem Radius r und der Durchdringung je dreier Zellwandfolien der Stärke t im Bereich ihrer gemeinsamen "Schnittlinien” erhält man algebraisch die Komponente des gesamten Porenanteils n = 1- 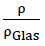 eines Körpers aus dem Modellschaumglas "TOP", die auf die von den Zellwandfolien aus Kugelschaumglas eingeschlossenen Gasphasen entfällt zu
eines Körpers aus dem Modellschaumglas "TOP", die auf die von den Zellwandfolien aus Kugelschaumglas eingeschlossenen Gasphasen entfällt zu
24)nZ=n⋅ω=1− SV⋅t
Berücksichtigt man aber den Volumenanteil der in Bild Nr. 15 eingezeichneten Plateauränder und den Einfluss der oben erwähnten Ueberschneidungen der Zellwandfolien, so kommen zur rechten Seite des obigen Zusammenhanges noch zwei zusätzliche Glieder hinzu! Es ergibt sich dann der Porenanteil der von den Zellwandfolien eingeschlossenen polyederförmigen Gasblasen zu
25)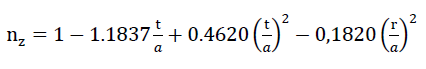
Der Zusammenhang zwischen dem Porenanteil n des Modellschaumglases "TOP" und den in Kapitel A, Abschnitt Nr. 2, definierten Parametern nz und n* wird durch die einfache volumetrische Gleichung
26)n=n∗+(1−n∗)⋅nz
gegeben.
Trotz der Tatsache, dass die Kontur der bereits weiter oben eingeführten Plateauränder eigentlich nur vom Gasblasendruck und den Oberflächenspannungen während dem Schäumprozess abhängt, wurden die Radien der kreiszylinderförmig
angenommenen Plateauränder willkürlich zu
r = 2 t
festgelegt, wobei t die Stärke der ebenflächig angenommenen Wandfolien des Modellschaumglases bedeutet.
Begründung:
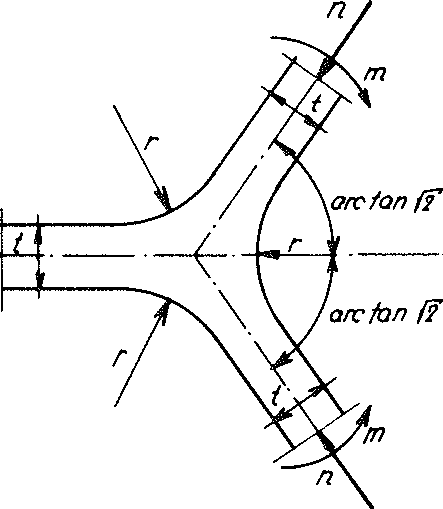
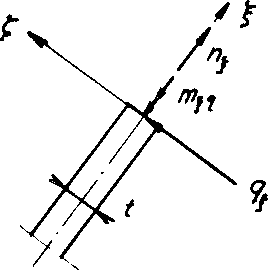
Bild Nr. 16 Mit Schnittkräften beanspruchter Plateaurand
Der Einfluss eines Biegemoments m sowie einer Normalkraft n auf den Spannungszustand im Plateaurand (siehe Darstellung auf Bild Nr. 16) wurde unter Zugrundelegung eines ebenen Verzerrungszustandes (EVZ) in der Normalebene zur Schnittlinie der Mitteiebenen dreier Zellwandfolien numerisch untersucht. Diese Voraussetzung eines ebenen Verzerrungszustandes ist sicher zulässig, da die Länge a der Schnittlinie der Mittelebenen dreier beliebiger benachbarter Kugelschaumwandfolien viel grösser als ihre Wandstärke t ist. Der Spannungszustand zeigte sich bei dieser Annahme r = 2 t so ausgewogen, dass ohne weiteres die Kerbwirkung des Plateaurandes praktisch vernachlässigt werden darf.
Würde jedoch im Gegensatz zu obiger Annahme r = 0 betragen, so bekäme man im Sinne Neubers eine Formzahl α, die beim Biegemoment m 1,62 und bei der Normalkraft n 1,69 betragen würde.
Folgerung aus obiger Annahme r = 2 t:
Da sich dann unter der Annahme r = 2 t die obige Gleichung Nr. 25 zum Ausdruck
27)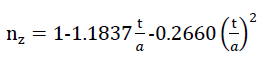
spezialisiert, erhält man unter Berücksichtigung des Zusammenhanges zwischen dem Porenanteil n und den Parametern nz und n* nach Gleichung Nr. 26 die Dichte des Polyederschaumglases zu
28)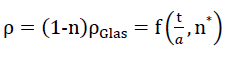
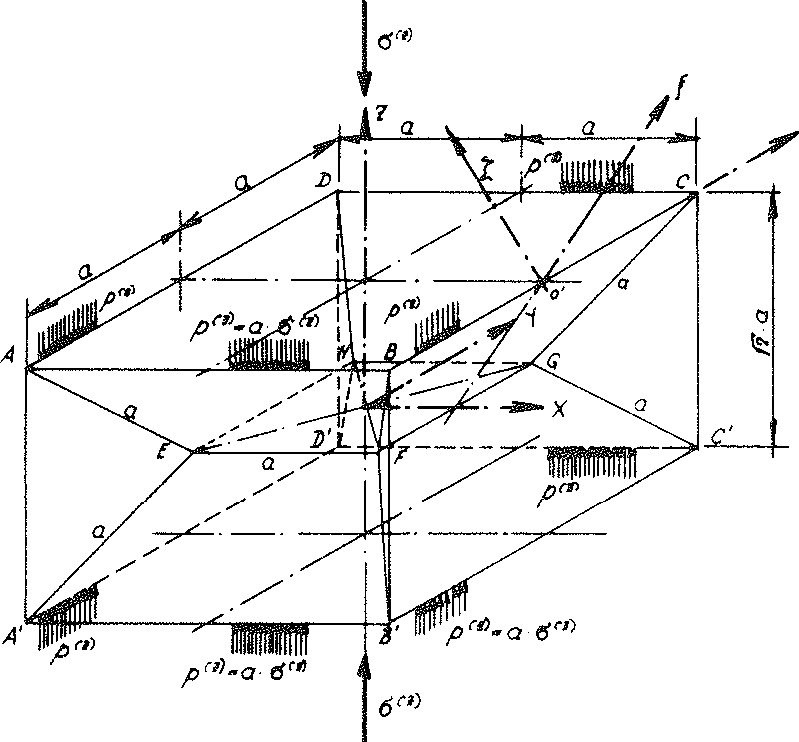
Bild Nr. 18 Die mit den Linienlasten ρ(z) aus der äusseren Belastung σ(z) beanspruchte Subeinheit des Modellschaumglases "TOP"
Jede Subeinheit des Zellwerkes aus den ebenen Mittelflächen der Zellwandfolien des allseitig unbegrenzten Modellschaumglases "TOP" ist gleichberechtigt. Deshalb kann jedes mit einer Subeinheit verbundene geeignete Koordinatensystem als ruhend betrachtet und damit für den ganzen Polyederschaumglaskörper als ruhendes Bezugssystem gewählt werden. Folglich wird bezüglich den weiteren Untersuchungen die in obigem Bild Nr. 18 dargestellte Subeinheit benutzt und das mit ihr verbundene Koordinatensystem x, y, z für den ganzen Modellschaumglaskörper als ruhendes Bezugssystem vorausgesetzt.
Grund- und Aufriss des Zellwerkes des Modellschaumglases (Bild Nr. 11 und Nr. 12) zeigen, wie die parallel zu den Achsen x, y, z des ruhenden Bezugssystems verlaufende Kanten (z.B.  ) der Subeinheit je auf einer zweizähligen Drehachsee des ganzen Modellschaumglases liegen. Vor, während und nach Belastung des Modellschaumglases mit der in x- und y- Richtung unbegrenzten äusseren Flächenlast σ(z) bleiben die Symmetrieeigenschaften dieser Drehachsen erhalten und sie bleiben gerade.
) der Subeinheit je auf einer zweizähligen Drehachsee des ganzen Modellschaumglases liegen. Vor, während und nach Belastung des Modellschaumglases mit der in x- und y- Richtung unbegrenzten äusseren Flächenlast σ(z) bleiben die Symmetrieeigenschaften dieser Drehachsen erhalten und sie bleiben gerade.
Die z - Achse des mit der Subeinheit verbundenen Koordinatensystems x, y, z bleibt vor, während und nach der Belastung σ(z) eine vierzählige Drehachse des Modellschaumglases "TOP". Aus diesem Grunde brauchen die geometrischen Randbedingungen für die gedanklich aus seinem Zellwerk herausgelöste Subeinheit nur am Beispiele ihrer Ränder 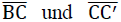 ausführlich behandelt zu werden. Da jede Teilfläche der Subeinheit des Modellschaumglases eine Mittelfläche einer ebenen Zellwandfolie bildet, kommt ihr herauslösen aus dem Zellwerk des Modellpolyederschaumglases einem gleichzeitigen Herausschneiden eines aus ebenen Platten bestehenden Flächentragwerkes (= Materielle Subeinheit) gleich. Die Randbedingungen für die an den Schnitträndern dieses Tragwerkes auf tretenden Momente und Kräfte können aus den geometrischen Bedingungen mit Hilfe der Platten beziehungsweise Scheibentheorie gefunden werden.
ausführlich behandelt zu werden. Da jede Teilfläche der Subeinheit des Modellschaumglases eine Mittelfläche einer ebenen Zellwandfolie bildet, kommt ihr herauslösen aus dem Zellwerk des Modellpolyederschaumglases einem gleichzeitigen Herausschneiden eines aus ebenen Platten bestehenden Flächentragwerkes (= Materielle Subeinheit) gleich. Die Randbedingungen für die an den Schnitträndern dieses Tragwerkes auf tretenden Momente und Kräfte können aus den geometrischen Bedingungen mit Hilfe der Platten beziehungsweise Scheibentheorie gefunden werden.
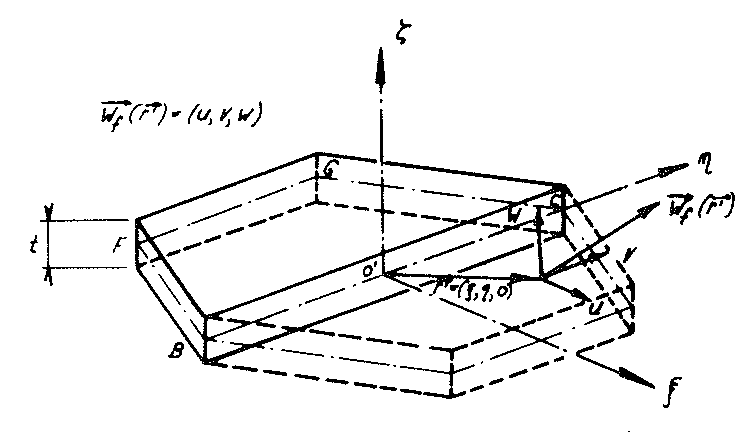
Bild Nr. 19 Hexagonförmige ebene Zellwandfolie des Modellschaumglases "TOP"
Wie Bild Nr. 19 zeigt, ist die trapezförmige Fläche 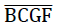 der Subeinheit als Hälfte der Mittelfläche einer hexagonförmigen ebenen Zellwandfolie
der Subeinheit als Hälfte der Mittelfläche einer hexagonförmigen ebenen Zellwandfolie
(der Stärke t) des Modellpolyederschaumglases zu betrachten. In den Bildern Nr. 18, Nr. 19 und Nr. 20 wurde das mit der betrachteten Platte (= Zellwandfolie) fest verbundene rechtshändige Koordinatensystem 𝜉, η, ζ eingetragen, dessen Ursprung o′ im Mittelpunkt der Srecke BC liegt.
- 1)Ein ebener Flächenträger, der nur durch Kräfte in seiner Ebene beansprucht wird und dessen Mittelfläche bei der Formänderung eben bleibt, wird Scheibe genannt. Derselbe Körper wird als Platte bezeichnet, wenn er einer Belastung unterworfen ist, die eine Verwölbung der ursprünglich ebenen Fläche hervorruft. Ebene Flächenträger, welche gleichzeitig als Scheibe und als Platte beansprucht sind, werden auch als Platten bezeichnet.
alle Punkte P (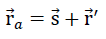 ) auf der Strecke BC translatorisch um
) auf der Strecke BC translatorisch um 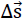 s in die neue Endlage mit dem Fahrstrahl
s in die neue Endlage mit dem Fahrstrahl
31)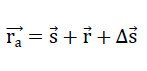
bewegen ( 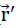 || η - Achse).
|| η - Achse).
Die Komponentenschreibweise der jedem Punkt P ( 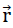 =(ξ,η,ζ)) der Plattenmittelebene bezüglich dem System ξ, η, ζ zugeordnete Relativverschiebung lautet (siehe Bild Nr. 19)
=(ξ,η,ζ)) der Plattenmittelebene bezüglich dem System ξ, η, ζ zugeordnete Relativverschiebung lautet (siehe Bild Nr. 19)
 (
( =(ξ,η,o))=(u(ξ,η,o),ν(ξ,η,o),w(ξ,η,o))
=(ξ,η,o))=(u(ξ,η,o),ν(ξ,η,o),w(ξ,η,o))
Die beiden Komponenten u und ν beschreiben die ebenen Verzerrungen der Plattenmittelebene (Scheibenbeanspruchung) und w die zu ihr normalen Durchbiegungen (Plattenbeanspruchung). Infolge der Zweizähligkeit der η - Achse des Systems ξ, η, ζ gelten für diese Verschiebungen u, ν und w die Symmetriebedingungen
32)
- (a) u(ξ,η,o)=−u(−ξ,η,o)
- (b) ν(ξ,η,o)=+ν(−ξ,η,o)
- (c) w(ξ,η,o)=−w(−ξ,η,o)
Die Durchbiegungen w (ξ, η, o) weisen im Vergleich zur Plattenstärke t sehr kleine absolute Beträge auf. Daher können die durch sie veursachten Verzerrungen der Plattenmittelebene vernachlässigt werden. Das bedeutet, dass der ebene Spannungszustand der ursprünglich ebenen Platte (Membranspannungszustand aus Scheibenwirkung) durch die seitlichen Auslenkungen w (ξ, η, o) nicht beeinflusst wird. Dies kommt aber einer Entkoppelung des gemischten Problems aus Platten- und Scheibenwirkung gleich! Somit können die Randbedingungen für die Membranbeanspruchung (Scheibe) und die Biegebeanspruchung1) am Rand  der Materiellen Subeinheit getrennt formuliert werden.
der Materiellen Subeinheit getrennt formuliert werden.
- 1)Es können aber für jeden Ort der Plattenberandung nur zwei Randbedingungen erfüllt werden.
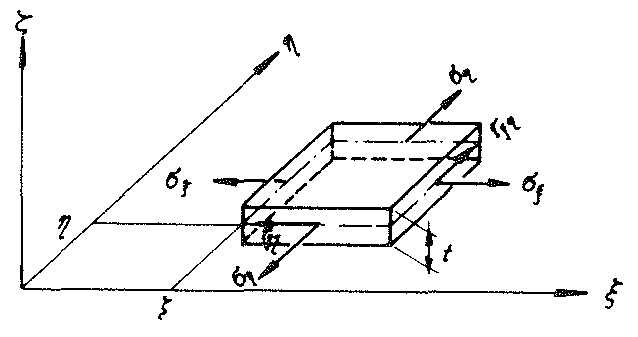
Bild Nr. 21 Element dξ ⋅ dη⋅t der Hexagonplatte der Stärke t
- Plattensteifigkeit :D =
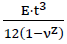
- E :Elastizitätsmodul,ν :Querdehnungszahl
Bild Nr. 21 zeigt das Element dξ ⋅ dη ⋅ t der betrachteten Hexagonplatte, deren Mitteifläche infolge der Flächenbelastung p (ξ,η) eine Durchbiegung w(ξ,η) erleidet. Diese beiden Grössen erfüllen die bekannte biharmonische Plattengleichung (12)
33)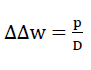
sowie die Randbedingungen.
Da nur an den verschieblichen Rändern der betrachteten Platte Kräfte angreifen, betragen für alle ihre Punkte die Flächenbelastungen p (ξ,η)=0. Die Plattengleichung vereinfacht sich damit zur homogenen biharmonischen Gleichung
34)ΔΔw=0
Die am Plattenelement dξ⋅dη⋅t auf Bild Nr. 21 angreifenden und auf die Längeneinheit der Schnittfläche bezogenen Schnittkräfte betragen
Aus Gleichung Nr. 32 c kann für ξ=0 auf das Verschwinden der zweiten partiellen Ableitung der Biegefläche w(ξ,η,o) nach der Variablen ξ geschlossen werden. Es gilt daher
36)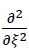 w(0,η,o)=0
w(0,η,o)=0
Die Tatsache, dass bei der hier betrachteten äusseren Belastung σ(z) die auf der η - Achse liegende Strecke  der Plattenmittelebene gerade bleibt, manifestiert sich mit der Aussage
der Plattenmittelebene gerade bleibt, manifestiert sich mit der Aussage
37)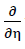 w(0,η,o)=0
w(0,η,o)=0
Werden diese letzten beiden Bedingungen in die Gleichungen Nr. 33 eingesetzt, so ergeben sich die auf die Einheitslänge der Schnittfläche ξ=0 der Trapezplatte  wirkenden Schnittmomente (Biegungsmomente und Drillungsmomente) zu
wirkenden Schnittmomente (Biegungsmomente und Drillungsmomente) zu
mξ(o,η) = mη(o,η) = 0,
mξη(o,η) ≠ 0 und die Scherkräfte zu
qξ(o,η) ≠ 0 sowie qη(o,η)=0 ;
d.h. infolge Biegung greifen am Schnitt ξ=0 der Platte nur auf die Längeneinheit der Schnittfläche bezogene Scherkräfte qξ und Drillungsmomente mξη an.
Weiter obern wurde nachgewiesen, dass die Mittelebene der betrachteten Hexagonplatte (siehe Bild Nr. 19) infolge der äusseren Belastung σ(z) des Modellschaumglases nicht nur Durchbiegungen w(ξ,η) sondern auch ebene Verzerrungen (u(ξ,η),ν(ξ,η)) erleidet.

Bild Nr. 22
Bild Nr. 22 zeigt ein Element dξ ⋅ dη ⋅ t der betrachteten Hexagonplatte mit den an ihm angreifenden Membranspannungen σξ,ση und τξη=τηξ
Diese Spannungen müssen die Gleichgewichtsbedingungen
38)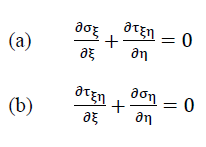
des ebenen Spannungszustandes erfüllen. Sie können mit der Funktion F (ξ, η) wie folgt ausgedrückt werden:
39)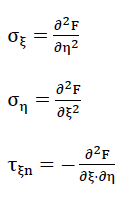
F(ξ,η), die als sogenannte Airy'sche Spannungsfunktion benannt wird, hat die Scheibengleichung
40)ΔΔF=0
und sämtliche Randbedingungen des Problems zu erfüllen.
Die Scheibengleichung gilt für jeden isotropen Werkstoff der dem Hooke'schen
Gesetz gehorcht. In ihr sind die Gleichgewichtsbedingungen (Gleichungen Nr. 38), geomterischen Bedingungen und Spannungsdehnungsgleichungen in einer einzigen Differentialgleichung zusammengefasst.
Infolge den Symmetriebedingungen Nr. 32a und Nr. 32b verschwinden auf der Diagonalen 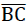 der "Plattenmittelebene" auch die Winkeländerungen
der "Plattenmittelebene" auch die Winkeländerungen
41)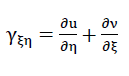
zwischen den Linienelementen dξ und dη ; d.h. es gilt γξη=0 .
Für die Platte aus idealelastischem Grundmaterial besteht die bekannte Relation
42)𝜏𝜉𝜂=𝐺⋅𝛾𝜉𝜂
zwischen den Schubspannungen τξη und den Winkeländerungen γξη mit G= 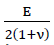 Folglich betragen für alle Punkte der Schnittfläche ξ=0 die Schubspannungen τξη(o,η)=0 .
Folglich betragen für alle Punkte der Schnittfläche ξ=0 die Schubspannungen τξη(o,η)=0 .
Durch Einsetzen in die Gleichgewichtsbedingung Nr. 38a kann somit bewiesen werden, dass auf allen Punkten der Schnittfläche ξ = 0 nur die Hauptnormalspannungen σξ(o,η)=f(η) und ση(o,η) = konstant auftreten können.
A priori kann festgestellt werden, dass auf der Längeneinheit des Randes 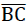 der Materiellen Subeinheit variable Normalkräfte nξ=σξ(o,η,ζ)⋅t , variable Scherkräfte qξ=qξ(o,η) und variable Drillungsmomente mξη=mξη(o,η) angreifen!
der Materiellen Subeinheit variable Normalkräfte nξ=σξ(o,η,ζ)⋅t , variable Scherkräfte qξ=qξ(o,η) und variable Drillungsmomente mξη=mξη(o,η) angreifen!
Somit kann die Strecke 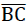 als eine geradebleibende Gelenklinie betrachtet werden!
als eine geradebleibende Gelenklinie betrachtet werden!
Da die z - Achse der betrachteten Subeinheit mit einer vierzähligen Drehachse des Modellschaumglases "TOP" zusammenfällt und alle Subeinheiten gleichberechtigt sind, kann das soeben gesagte auf alle seine zu den Achsen x und y des ruhenden Bezugssystem x, y, z parallel verlaufenden Gelenklinien übertragen werden.
Wie der Grund- und Aufriss auf Bild Nr. 11 und Nr. 12 zeigen, liegt das ebene Dreieck 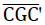 der Subeinheit in einer Symmetrieebene und seine Seite
der Subeinheit in einer Symmetrieebene und seine Seite 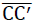 auf einer zweizähligen Drehachse des Modellschaumglases "TOP". Das Dreieck bildet somit die Hälfte der Mittelebene einer Quadratplatte der Materiellen Subeinheit der Stärke t (siehe Bild Nr. 23).
auf einer zweizähligen Drehachse des Modellschaumglases "TOP". Das Dreieck bildet somit die Hälfte der Mittelebene einer Quadratplatte der Materiellen Subeinheit der Stärke t (siehe Bild Nr. 23).
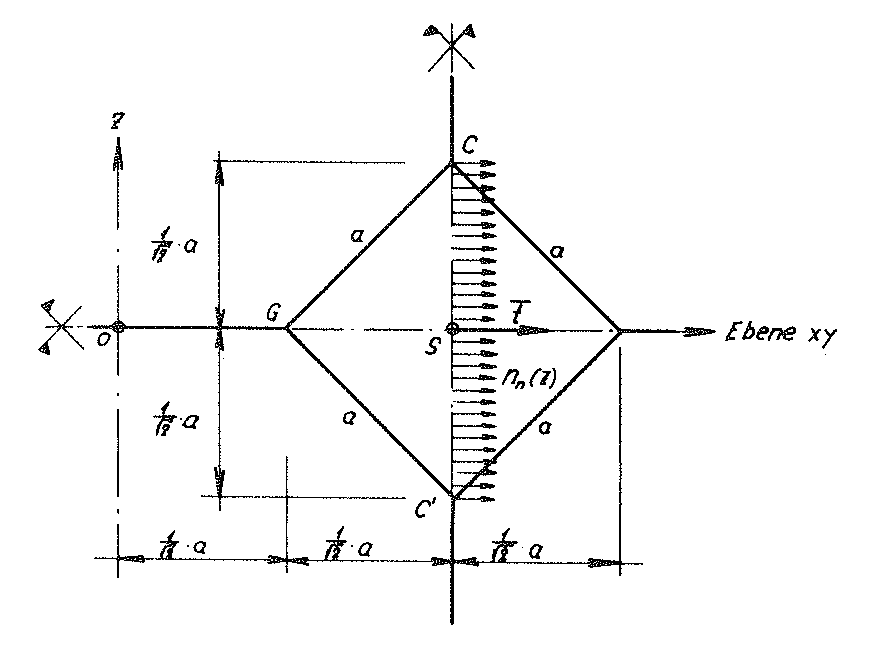
Bild Nr. 23 Schnitt der Subeinheit des Modellschaumglases "TOP" mit ihrer durch die Punkte C, G und C' bestimmten Symmetrieebene; S: Schwerpunkt
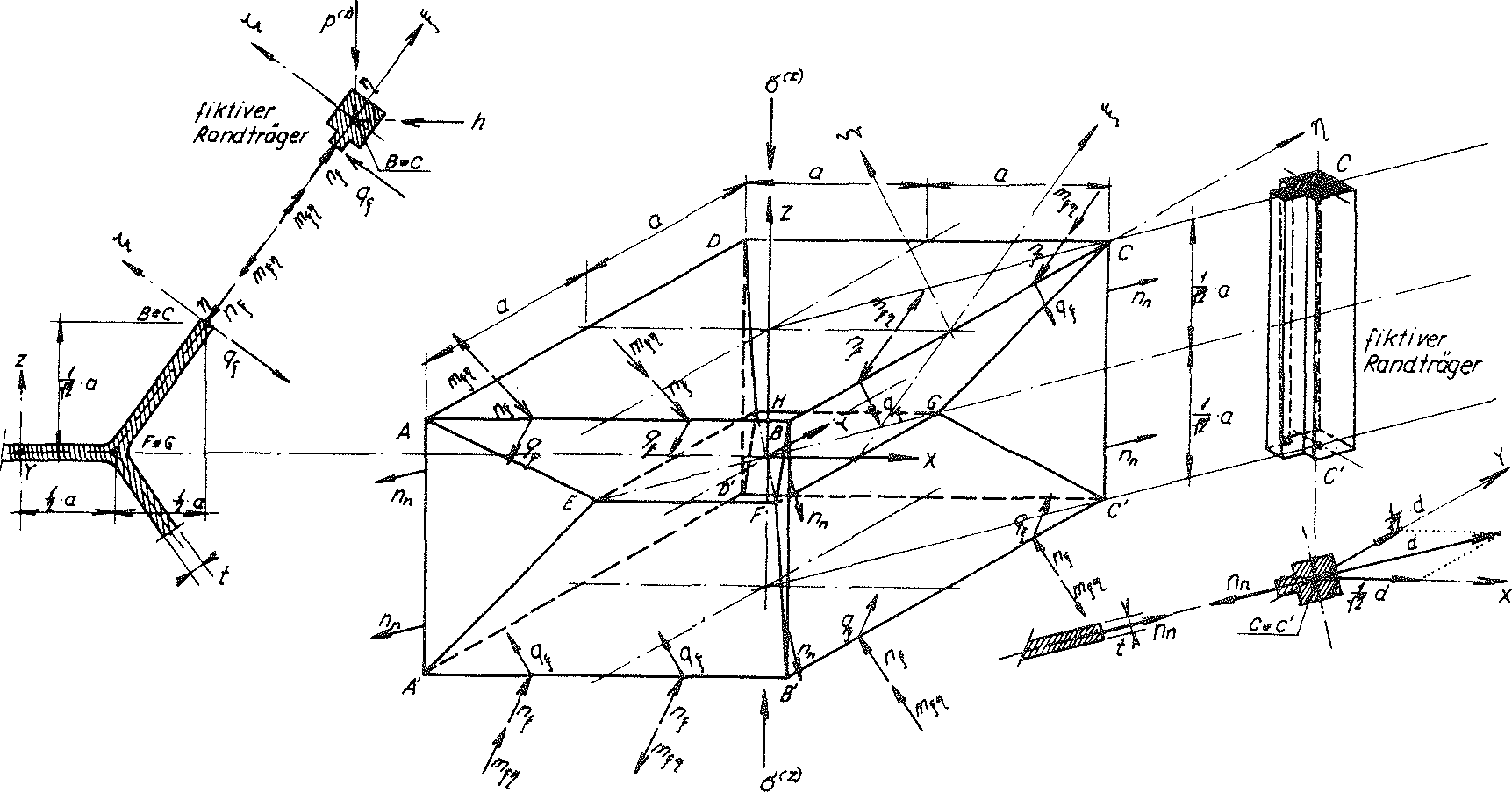
Bild Nr. 24 Die auf die Materielle Subeinheit des Modellschaumglases "TOP" wirkenden Schnittkräfte unter der äusseren Belastung σ(z)
Die obigen Symmetrieeigenschaften der betrachteten Quadratplatte gehen beim Aufbringen der Belastung σ(z) des Modellschaumglases nicht verloren. Aus diesem Grunde bleibt ihre durch das Dreieck CC'G bestimmte Mittelfläche als Teil der obigen Symmetrieebene eben. Sie erleidet nur eine Starrkörpertranslation 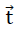 = (tx,ty=tx,o) 1) und zu ihrer Mittelebene symmetrische Verformungen.
= (tx,ty=tx,o) 1) und zu ihrer Mittelebene symmetrische Verformungen.
Da die Diagonale 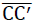 der Mittelfläche der betrachteten Quadratplatte (Scheibe) auf einer zweizähligen Drehachse liegt, kann analog wie beim Rand
der Mittelfläche der betrachteten Quadratplatte (Scheibe) auf einer zweizähligen Drehachse liegt, kann analog wie beim Rand 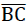 der Materiellen Subeinheit (Rand der Hexagonplatte) nachgewiesen werden, dass an ihm nur auf die Längeneinheit bezogene variable Normalkräfte nn=nn(z) mit Wirkungslinien in Plattenmittelebene angreifen können.
der Materiellen Subeinheit (Rand der Hexagonplatte) nachgewiesen werden, dass an ihm nur auf die Längeneinheit bezogene variable Normalkräfte nn=nn(z) mit Wirkungslinien in Plattenmittelebene angreifen können.
Die z - Achse der Subeinheit bleibt vor, während und nach Belastung mit σ(z) eine vierzählige Drehachse des Modellschaumglases "TOP". Daher kann gefolgert werden, dass an allen vertikalen Rändern der Materiellen Subeinheit unter der äusseren Belastung σ(z) nur variable Normalkräfte nn(z) mit rechtwinklig zur z - Achse stehenden Wirkungslinien angreifen können.
Bild Nr. 24 zeigt eine Materielle Subeinheit des Modellschaumglases "TOP" unter der äusseren Belastung σ(z) . Ebenfalls wurden dort, die auf die Längeneinheit ihrer Ränder wirkenden Schnittkräfte nξ,qξ,mξη und nn eingetragen.
Wir versehen alle Ränder dieser Materiellen Subeinheit mit fiktiven Trägern, die keine zusätzlichen Zwängungen verursachen dürfen (siehe Bild Nr. 24)! Ein solcher Träger ist biegestarr (EJξ=EJζ=∞), torsionsweich (GJP=0) und zugweich (EF=0). Infolge diesen besonderen elastischen Eigenschaften der Randträger können die Beanspruchungen mξη,qξ,nξ und nn am Rand der unverstärkten Materiellen Subeinheit durch die an der verstärkten Materiellen Subeinheit angreifenden konstanten Linienlasten p(z), h und 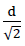 ersetzt werden (siehe Bild Nr. 24a). Dabei werden die geometrischen Randbedingungen nach den Gleichungen Nr. 32 eingehalten.
ersetzt werden (siehe Bild Nr. 24a). Dabei werden die geometrischen Randbedingungen nach den Gleichungen Nr. 32 eingehalten.
- 1)Die Wirkungslinie des Vektors
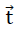 fällt mit der durch die Punkte O und S definierten Geraden zusammen.
fällt mit der durch die Punkte O und S definierten Geraden zusammen.
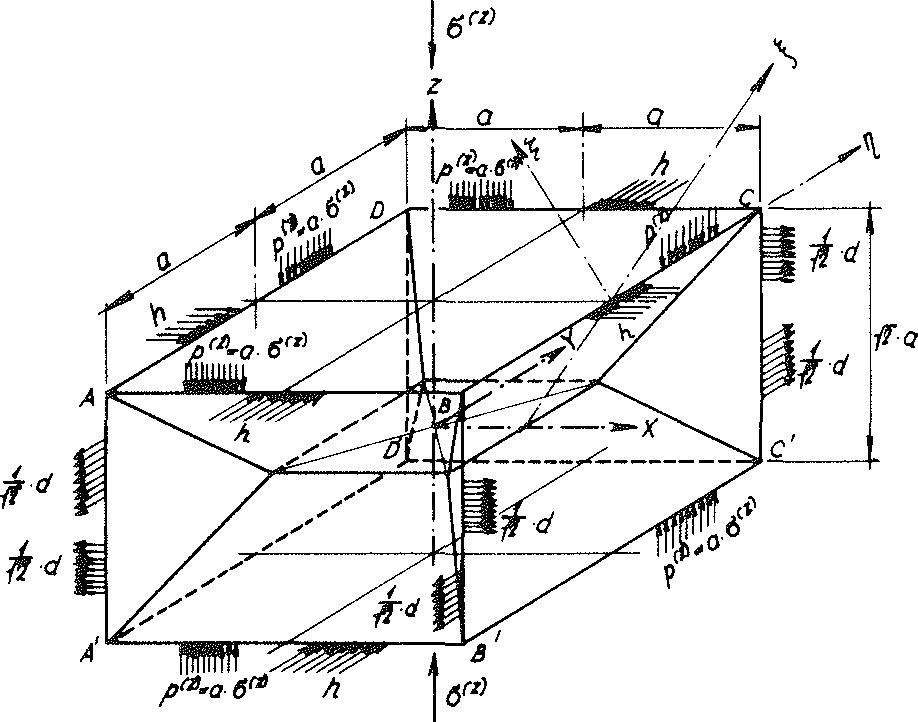
Bild Nr. 24a Die mit den Linienlasten p(z) aus der äusseren Belastung σ(z) beanspruchte Materielle Subeinheit des Modellschaumglases "TOP"
Auf Bild Nr. 24a wurden sämtliche an den Rändern der verstärkten Materiellen Subeinheit in Richtung der Koordinatenachsen x, y, z angreifende Linienlasten eingetragen!
Da das Schaumglas nur durch die äussere Flächenlast σ(z) beansprucht wird, müssen die Summen aller in den Schnitten x=±a angreifenden Kräfte Xi verschwinden (ΣXi=o). Das Analoge gilt auch für die Schnitte y=±a. Dann beträgt
431))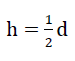
In den Ebenen x = ± a und y = ± a der verstärkten Materiellen Subeinheit bilden die fiktiven Randträger biegestarre Rahmen. Daher kann gefolgert werden, dass der Wert 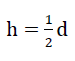 keinen Einfluss auf das Beanspruchungsbild
keinen Einfluss auf das Beanspruchungsbild
- 1)
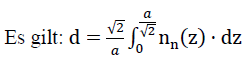
der so "verstärkten" Materiellen Subeinheit ausübt. Er kann somit für die weiteren Betrachtungen Null gesetzt werden. Es verbleiben dann nur noch die auf die Ränder der verstärkten Materiellen Subeinheit (siehe auch Bild Nr. 18) wirkenden vertikalen Linienlasten
44)p(z) = а ⋅ σ(z)
Gemäss der Hypothese in Abschnitt 1.3.1 dieses Kapitels kann σ(z) dann der Druckfestigkeit 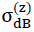 oder Zugfestigkeit
oder Zugfestigkeit 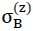 in Richtung z des Raumes gleichgesetzt werden, wenn die maximale Hauptzugspannung an irgend einer Stelle der inneren Oberflächen der Polyederzellen des Modellschaumglases "TOP" die Bruchfestigkeit σB(n∗) der als Kontinuum aufgefassten Kugelschaumglasplatten der Zellwandungen erreicht.
in Richtung z des Raumes gleichgesetzt werden, wenn die maximale Hauptzugspannung an irgend einer Stelle der inneren Oberflächen der Polyederzellen des Modellschaumglases "TOP" die Bruchfestigkeit σB(n∗) der als Kontinuum aufgefassten Kugelschaumglasplatten der Zellwandungen erreicht.
Da Glas und somit die aus diesem Grundmaterial aufgebauten Kugelschaumglasfolien des Polyederschaumglases ein sprödes Bruchverhalten aufweisen (siehe Abschnitt 1.1) und somit kein Abbau örtlicher Spannungsspitzen infolge Plastifizierung des Grundmaterials wie bei duktilen Stoffen stattfinden kann, sollen die Spannungszustände auf den Oberflächen der Zellwandfolien (siehe Hypothese in Abschnitt 1.3.1) zur Ermittlung der Festigkeiten 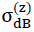 beziehungsweise
beziehungsweise 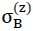 möglichst genau bekannt sein.
möglichst genau bekannt sein.
Aus diesem Grunde wurde für die erforderliche Spannungsanalyse die verstärkte Materielle Subeinheit des Modellschaumglases unter Benutzung verschiedener Symmetrieebenen auf ein Sechzehntel, wie auf Bild Nr. 25 dargestellt, beschränkt. Die so reduzierte Materielle Subeinheit wurde anschliessend für die Beanspruchung σ(z) in 340 finite Elemente eingeteilt.
Da gemäss Gleichung Nr. 28 in Abschnitt Nr. 1.3.2.1 die Dichte ρ des Modellschaumglases "TOP" neben der Dichte ρGlas seines Glasgrundmaterials nur vom Verhältnis 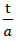 und vom Porenanteil n* der Kugelschaumglasfolien alleine abhängt, wurde für die Bestimmung der Bruchfestigkeiten
und vom Porenanteil n* der Kugelschaumglasfolien alleine abhängt, wurde für die Bestimmung der Bruchfestigkeiten 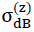 und
und 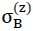 bei nullgesetztem Porenanteil n* jeweils nur das Verhältnis
bei nullgesetztem Porenanteil n* jeweils nur das Verhältnis 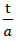 variiert (d.h. eigentlich nur die Dichte ρ). Die entsprechenden Werte
variiert (d.h. eigentlich nur die Dichte ρ). Die entsprechenden Werte 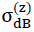 und
und 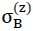 für andere Werte n∗≠0 konnten infolge der Oberflächenhypothese proportional umgerechnet werden. Die Zugfestigkeiten der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt Nr. 1.3.1 zu
für andere Werte n∗≠0 konnten infolge der Oberflächenhypothese proportional umgerechnet werden. Die Zugfestigkeiten der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt Nr. 1.3.1 zu
45)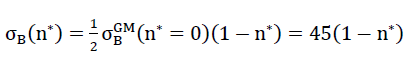
angenommen.
In der Tabelle auf Seite 52 wurden die auf diese Weise ermittelten Ergebnisse für die Festigkeitswerte 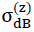 (n∗,ρ) und
(n∗,ρ) und 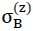 (n∗,ρ) zusammengestellt und in Bildern Nr. 26 und Nr. 27 graphisch dargestellt.
(n∗,ρ) zusammengestellt und in Bildern Nr. 26 und Nr. 27 graphisch dargestellt.
Besitzt die Zugfestigkeit 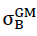 (n∗=0) des Glasgrundmaterials der Zellwandfolien nicht den hier für die Berechnung der Tabellenwerte und dem Aufzeichnen der Schaubilder für die Druckfestigkeiten und Zugfestigkeiten in Richtung z des Raumes angenommenen Wert von 90 N ⁄ mm2, sondern irgend einen anderen Wert
(n∗=0) des Glasgrundmaterials der Zellwandfolien nicht den hier für die Berechnung der Tabellenwerte und dem Aufzeichnen der Schaubilder für die Druckfestigkeiten und Zugfestigkeiten in Richtung z des Raumes angenommenen Wert von 90 N ⁄ mm2, sondern irgend einen anderen Wert 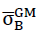 (n∗=0),so müssen die entsprechenden Tabellenwerte und die Ordinaten in den dazugehörenden Diagrammen nur mit dem Korrekturfaktor
(n∗=0),so müssen die entsprechenden Tabellenwerte und die Ordinaten in den dazugehörenden Diagrammen nur mit dem Korrekturfaktor 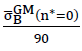 multipliziert werden.
multipliziert werden.
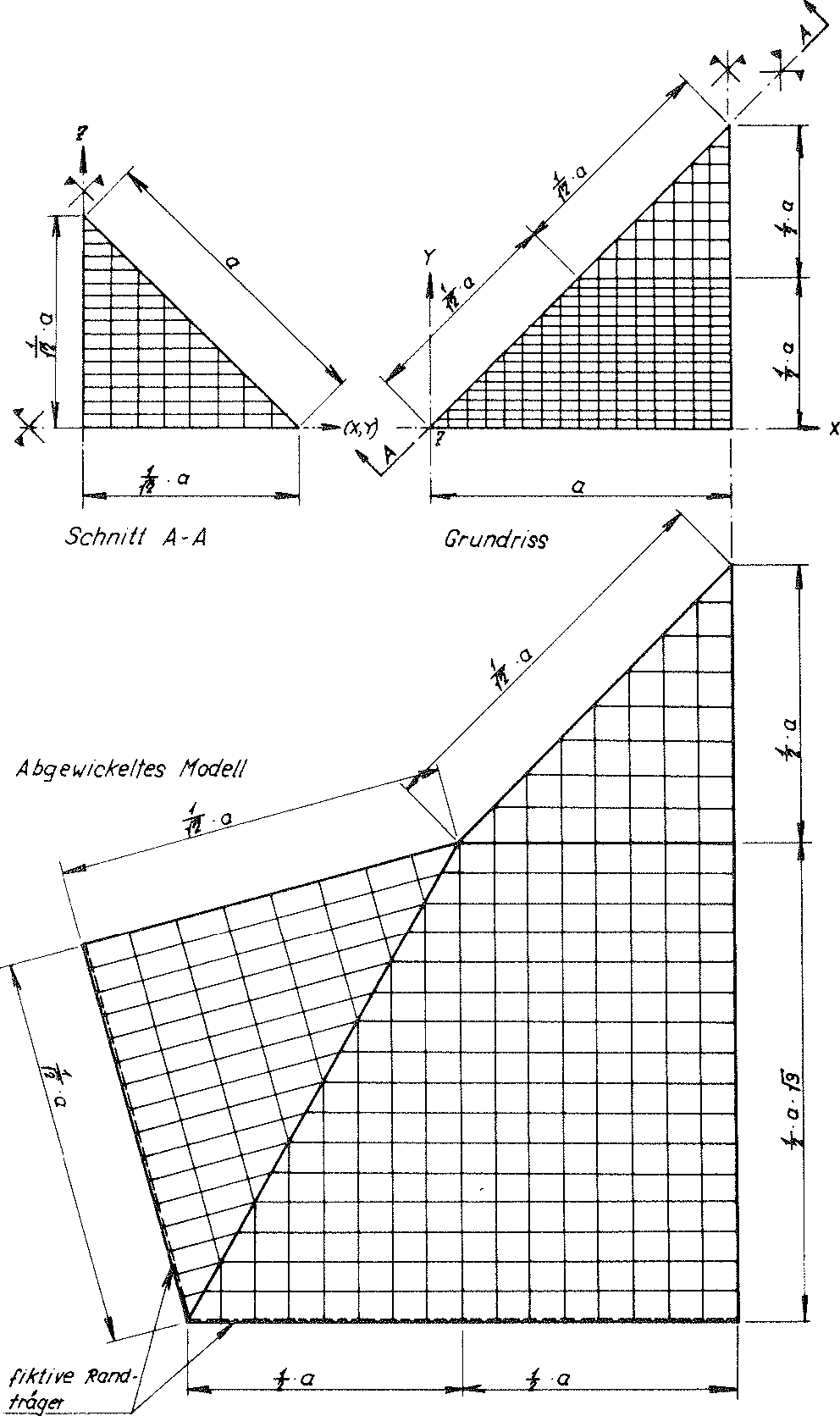
Bild Nr. 25 Aufteilung der durch Ausnutzung der Symmetrie reduzierten verstärkten Materiellen Subeinheit des Modellschaumglases "TOP" in 340 finite Elemente.
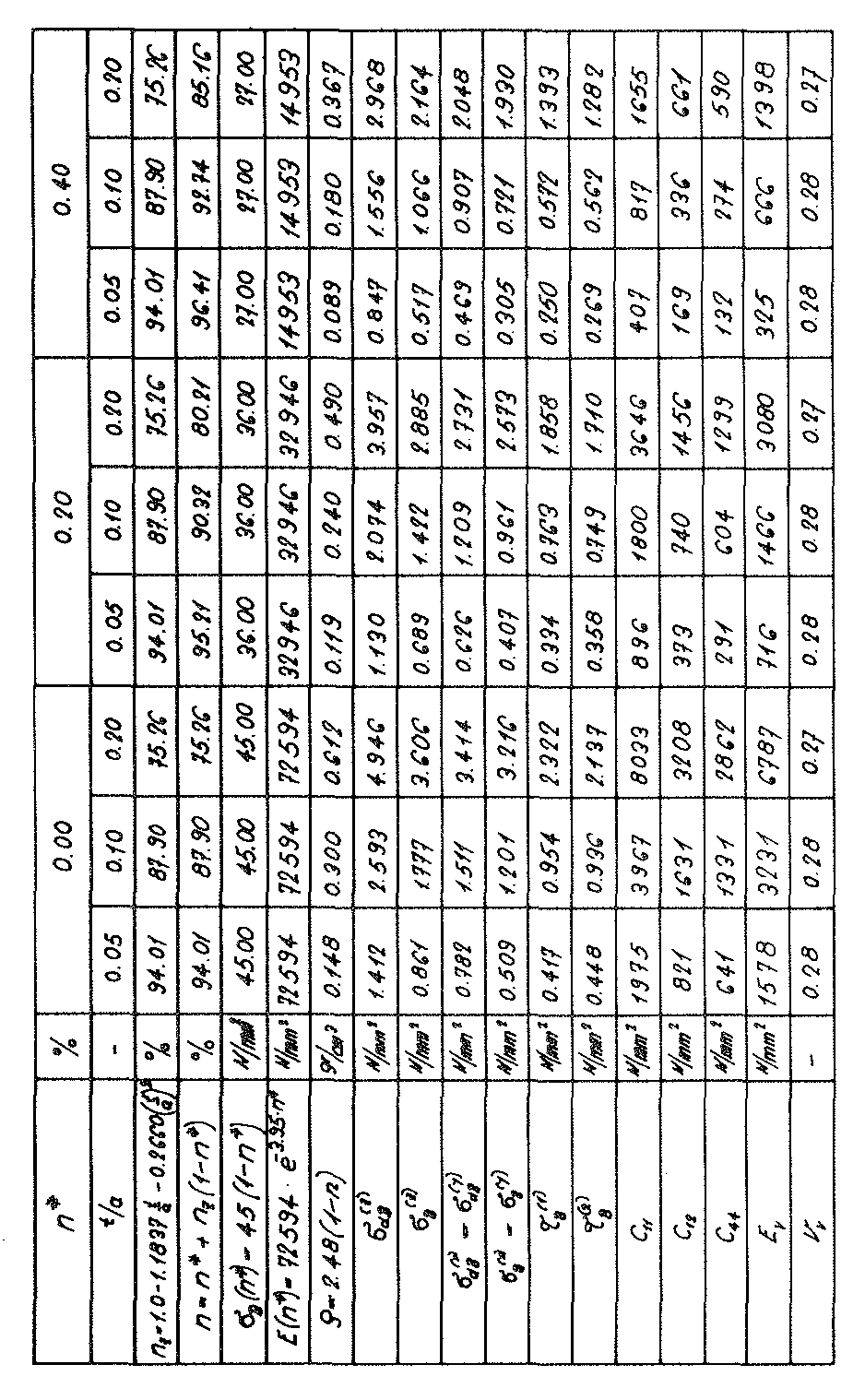
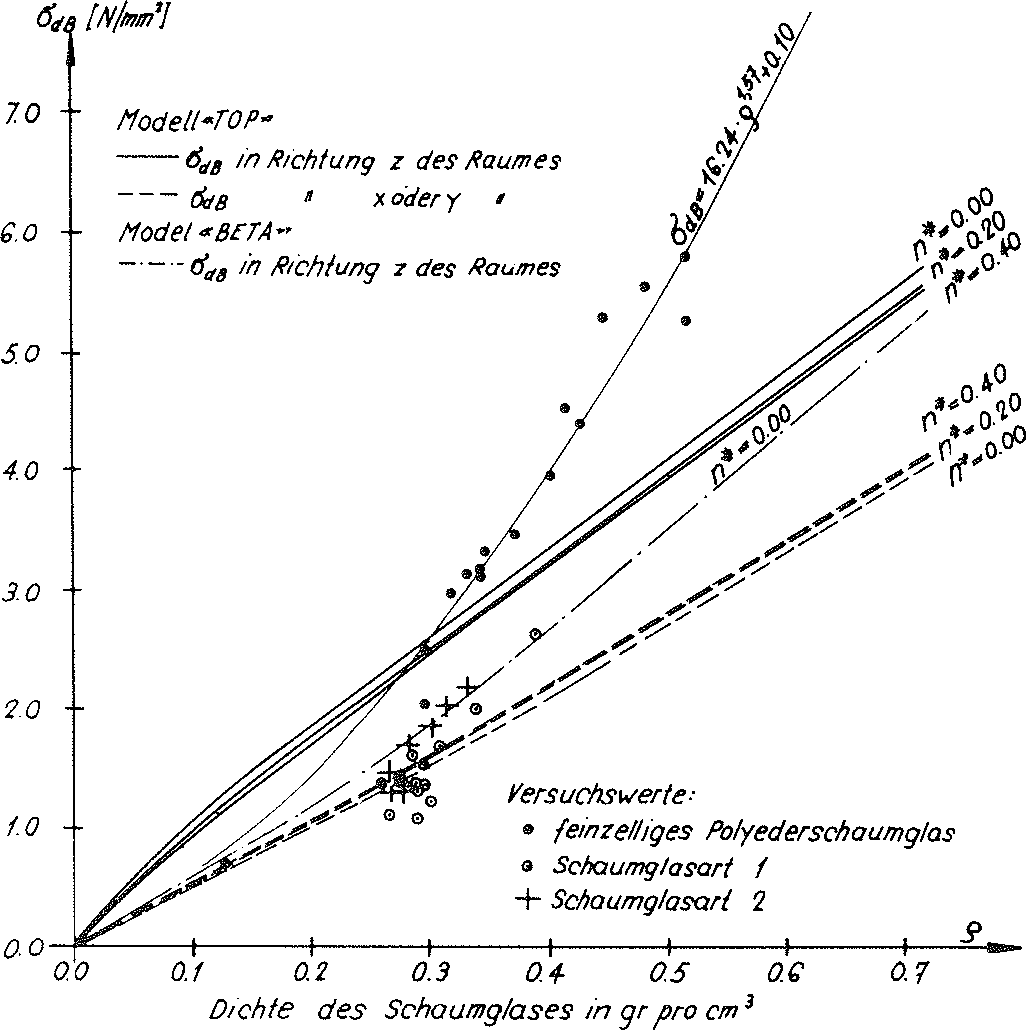
Bild Nr. 26 Die Druckfestigkeiten des Modellschaumglases "TOP"
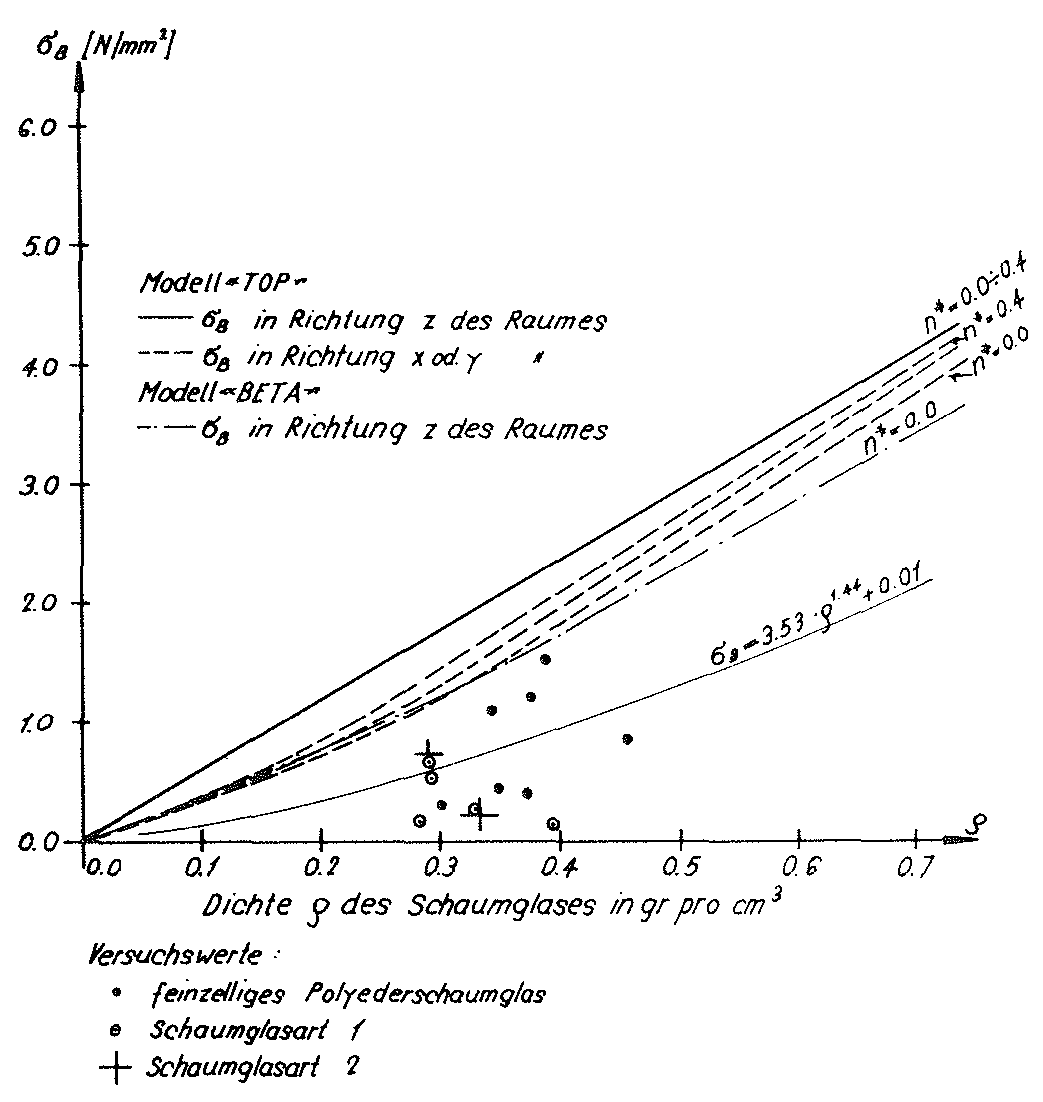
Bild Nr. 27 Die Zugfestigkeiten des Modellschaumglases "TOP”
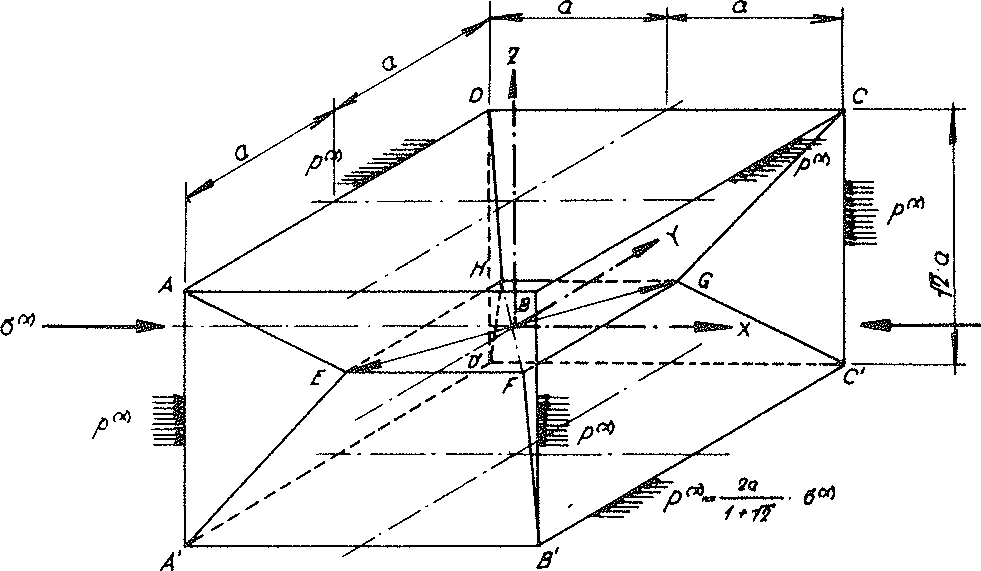
Bild Nr. 28 Die mit der Linienlast p(x) aus der äusseren Belastung σ(x) beanspruchte Subeinheit des Modellschaumglases "TOP"
Hier wird das Modellschaumglas "TOP" bezüglich dem in seinem Grund-und Aufriss in Bild Nr. 11 eingetragen kartesischen Koordinatensystem xyz in Richtung x des Raumes mit der in y- und z- Richtung unbegrenzten Flächenlast σ(x) beansprucht. Bei dieser Belastungsart liegen alle Kanten der in Bild Nr. 28 dargestellten Subeinheit vor, während und nach der Belastung auf zweizähligen Drehachsen. Dies ist - analog zu den Ausführungen im vorhergehenden Abschnitt - gleichwertig mit der Betrachtung aller Randlinien unserer Subeinheit als Teil einer Gelenkgeraden. Daher können auch hier alle Ränder der Materiellen Subeinheit mit den gleichen fiktiven Trägern verstärkt werden wie beim Belastungsfall σ(z).
Für die Ermittlung der Spannungen in der "verstärkten" Materiellen Subeinheit brauchen dann nur die an ihren Kanten angreifenden horizontalen konstanten
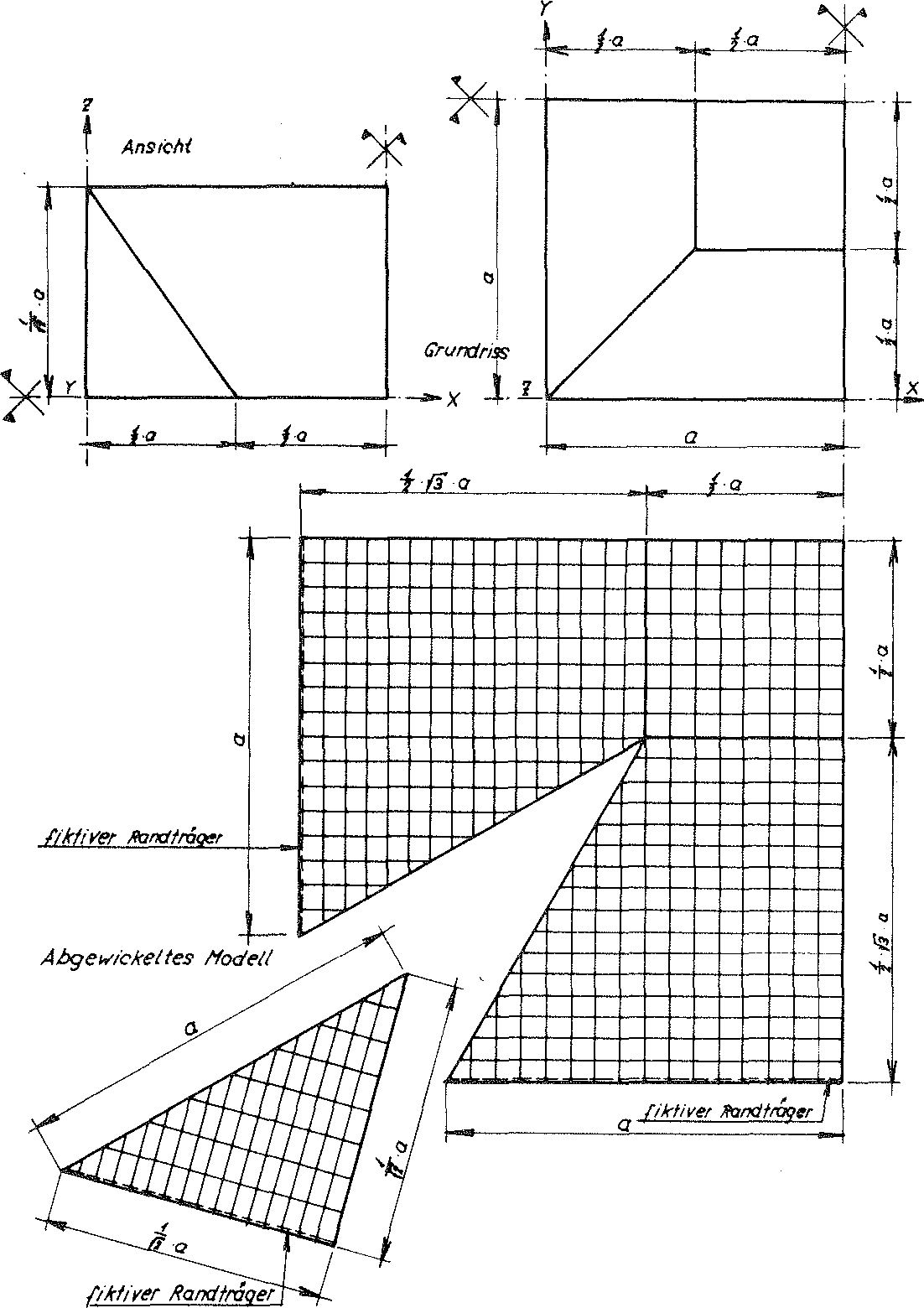
Bild Nr. 29 Aufteilung der durch Ausnutzung der Symmetrie reduzierten verstärkten Materiellen Subeinheit des Modellschaumglases "TOP", in 584 finite Elemente
Für jede beliebige Schnittebene E𝚒 durch das allseitig unbegrenzte Modellschaumglas "TOP" kann eine äussere Belastungskonfiguration gefunden werden, die in ihr eine reine Schubbeanspruchung τ𝚒 verursacht, nach der Oberflächenhypothese in Abschnitt Nr. 1.3.1 dieses Kapitels kann τ𝚒 dann der Schubfestigkeit τB𝚒 gleichgesetzt werden, wenn die maximale Hauptzugspannung an irgend einer Stelle der inneren Oberflächen der Polyederzellen des Modellschaumglases die Zugfestigkeit σB(n∗) der als Kontinuum aufgefassten Kugelschaumglasplatten der Zellwandungen erreicht. Da unbegrenzt viele Lagen der Schnittebenen durch das Modellschaumglas "TOP" existieren, sollte eigentlich nach dem kleinstmöglichen Wert τB𝚒 gefragt werden. Dieser müsste dann als Schubfestigkeit des Modellschaumglases definiert werden!
Hier soll nur eine Grobschätzung der Schubfestigkeiten erfolgen! Deshalb beschränken wir uns auf die zweiachsigen äusseren Beanspruchungen σ(x)und σ(z)=−σ(x). Diese können als Hauptspannungen aufgefasst werden und wurden - wie Bild Nr. 30 zeigt - auf die x - und z - Achse der Subeinheit des Modellschaumglases bezogen.
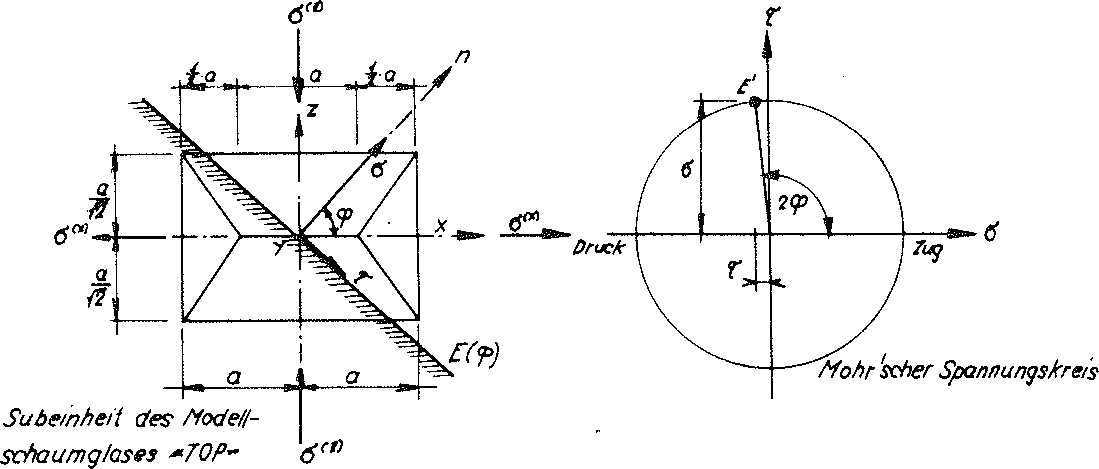
Bild Nr. 30
Die Ebene E(φ), deren in der (x,z) - Ebene liegende Normale n mit der x - Achse den Winkel φ einschliesst, wird durch die Normalspannungen σ und die Schubspannungen τ beansprucht. Die Beträge dieser Spannungen können am dazugehörenden Mohr'schen Spannungskreis als Koordinaten
des Punktes E' abgelesen werden. Der Spannungskreis auf Bild Nr. 30 zeigt, dass die Lagen der Ebenen reinen Schubes durch die auf die x - Achse der Subeinheit bezogenen Normalenwinkel φ=450 respektive φ=1350 festgelegt sind. Auf diese Weise wurden die normal aufeinanderstehenden Ebenen reinen Schubes E(φ=450) und E(φ=1350) gefunden. Die auf diese beiden Ebenen bezogenen Schubfestigkeiten weisen den gleichen Betrag 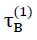 auf.
auf.
Werden die Komponenten σ(z) und σ(x)=−σ(z) der bereits behandelten äusseren Beanspruchungen durch ihre entgegengesetzt gleichen Werte −σ(x) und −σ(z) ersetzt, so erhält man in Bezug auf die normalspannungsfreien Ebenen E(φ=450) und E(φ=1350) eine vom früheren Wert verschiedene Bruchfestigkeit 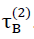
Die für die Ermittlungen der Schubfestigkeiten 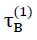 und
und 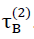 notwendigen Spannungsanalysen wurden am, auf Bild Nr. 29 dargestellten, "Achtel der verstärkten Materiellen Subeinheit" durchgeführt. Dabei wurde auch die gleiche Einteilung in 584 finite Elemente benutzt.
notwendigen Spannungsanalysen wurden am, auf Bild Nr. 29 dargestellten, "Achtel der verstärkten Materiellen Subeinheit" durchgeführt. Dabei wurde auch die gleiche Einteilung in 584 finite Elemente benutzt.
Da gemäss Gleichung Nr. 28 in Abschnitt Nr. 1.3.2.1. die Dichte ρ des Modellschaumglases "TOP" neben der Dichte ρGlas seines Grundmaterials nur vom Verhältnis 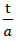 und vom Porenanteil n∗ der Kugelschaumglasfolien alleine abhängt, wurde für die Bestimmung von
und vom Porenanteil n∗ der Kugelschaumglasfolien alleine abhängt, wurde für die Bestimmung von 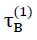 und
und 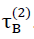 bei nullgesetztem Porenanteil n∗ jeweils nur das Verhältnis
bei nullgesetztem Porenanteil n∗ jeweils nur das Verhältnis 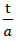 variiert; d.h. eigentlich nur die Dichte ρ. Die entsprechenden Festigkeiten
variiert; d.h. eigentlich nur die Dichte ρ. Die entsprechenden Festigkeiten 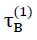 und
und 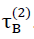 für andere Werte n∗≠0 konnten infolge der Oberflächenhypothese proportional umgerechnet werden. Die Zugfestigkeiten der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt 1.3.1 zu
für andere Werte n∗≠0 konnten infolge der Oberflächenhypothese proportional umgerechnet werden. Die Zugfestigkeiten der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt 1.3.1 zu
48)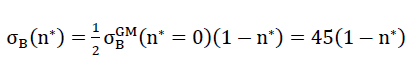
angenommen.
In der Tabelle auf Seite 52 wurden die auf diese Weise ermittelten Schubfestigkeiten 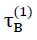 und
und 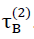 zusammengestellt und auf Bild Nr. 31 graphisch dargestellt.
zusammengestellt und auf Bild Nr. 31 graphisch dargestellt.
Besitzt die Zugfestigkeit 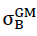 (n∗=0) des Glasgrundmaterials der Zellwandfolien nicht den hier für die Berechnung der Tabellenwerte und das Aufzeichnen der Schaubilder für die Schubfestigkeiten
(n∗=0) des Glasgrundmaterials der Zellwandfolien nicht den hier für die Berechnung der Tabellenwerte und das Aufzeichnen der Schaubilder für die Schubfestigkeiten 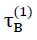 und
und 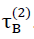 angenommenen Wert von 90 N/mm2, sondern irgend einen anderen Wert
angenommenen Wert von 90 N/mm2, sondern irgend einen anderen Wert 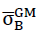 (n∗=0),so müssen die entsprechenden Tabellenwerte und die Ordinaten in den dazugehörenden Diagrammen nur mit dem Korrekturfaktor
(n∗=0),so müssen die entsprechenden Tabellenwerte und die Ordinaten in den dazugehörenden Diagrammen nur mit dem Korrekturfaktor 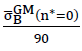 multipliziert werden.
multipliziert werden.
Bild Nr. 31 Die Schubfestigkeiten des Modellschaumglases "TOP“
Die Mittelflächen der Zellwandfolien des Modellschaumglases "TOP" bestehen aus den Oberflächen seiner periodisch angeordneten Elementarpolyeder. Da das integrale elastische Verhalten des Modellschaumglases "TOP" nur durch das Verhalten der einzelnen miteinander verträglichen kongruenten Materiellen Grundpolyeder bestimmt ist, können diese Materiellen Elementarpolyeder - unabhängig von ihrem inneren Aufbau - analog wie Einkristalle in der Kristallphysik behandelt werden.
Auf Grund der Symmetriebetrachtungen in Abschnitt Nr. 1.3.2.1. kann im Modellschaumglas "TOP" in parallelen Richtungen gleiches mechanisches Verhalten erwartet werden. Aus diesem Grunde kann das Modellschaumglas "TOP" als homogener anisotroper Körper bezeichnet werden. Solche kommen in der Natur als Kristalle vor.
Wie kann von den Symmetrieeigenschaften des Modellpolyederschaumglases "TOP" auf sein elastisches Verhalten geschlossen werden?
Eine Antwort auf diese Frage gibt das Prinzip von Neumann (13), das eigentlich nur für Kristalle aufgestellt wurde.
Es lautet:"Die Symmetrieelemente irgend einer physikalischen Eigenschaft eines Kristalles müssen die Symmetrieelemente der Punktgruppe (= Kristallklasse) des Kristalls enthalten."
Falls die Beziehung zwischen zwei physikalischen Eigenschaften eines Körpers in Richtung einer festen Achse nach Ausführung einer bestimmten Symmetrieoperation unverändert bleibt, so sagt man, die betreffende Grösse besitze dieses Symmetrieelement.
Beim Modellschaumglas "TOP" enthalten die Symmetrieelemente der elastischen Eigenschaften die Symmetrieelemente der Punktgruppe m 3 m des kubischen Kristallsystems.
Bezogen auf das rechtshändige kartesische Koordinatensystem (x1,x2,x3) auf Bild Nr. 13 lautet in Matrixschreibweise der Zusammenhang zwischen dem als Vektor geschriebenen Spannungstensor 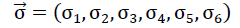 und dem als Vektor aufgefassten Verzerrungstensor
und dem als Vektor aufgefassten Verzerrungstensor 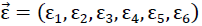
49).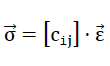
Dabei lautet die Matrix der Elastizitätsmoduln cij unter Berücksichtigung der Punktgruppe m 3 m (Kristallklasse) unseres Modellschaumglases "TOP"
50).
Die Komponenten des Spannungsvektors 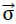 beziehungsweise Verzerrungsvektors
beziehungsweise Verzerrungsvektors 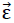 werden durch folgende Gleichheiten umbenannt:
werden durch folgende Gleichheiten umbenannt:
51).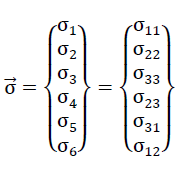
respektive
52).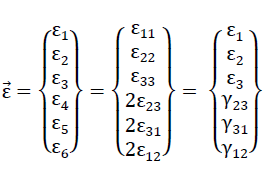
Die Komponenten σij des Vektors 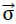 wurden im Volumenelement des Bildes Nr. 32 eingetragen, dabei gilt bei Abwesenheit von Körperdrehmomenten aus Gleichgewichtsgründen
wurden im Volumenelement des Bildes Nr. 32 eingetragen, dabei gilt bei Abwesenheit von Körperdrehmomenten aus Gleichgewichtsgründen
53).σij = σji
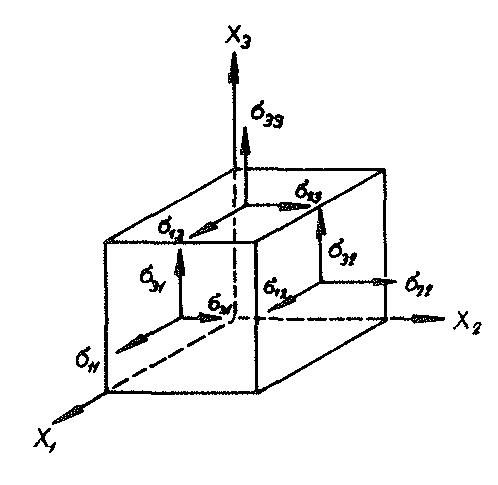
Bild Nr. 32 Volumenelement des als Kontinuum aufgefassten Modellschaumglases "TOP"
Die Verzerrungskomponenten εij werden durch die Gleichungen
54).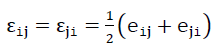
und
55).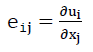
Bestimmt1).
- 1)eij bedeuten die beiden Komponenten eines Tensors [eij] 2. Stufe, der folgendermassen in den symmetrischen Verzerrungstensor [εij] und in den antimetrischen Tensor
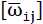 , der eine Starrkörperrotation bedeutet, zerlegt werden kann:
, der eine Starrkörperrotation bedeutet, zerlegt werden kann:
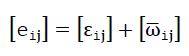
eij bedeutet hier die Ableitung der Verschiebung ui=f (x1,x2,x3) eines Punktes in Richtung Xinach der Koordinate Xj.
Die Werte für die Elastizitätsmoduln c11,c12 und c44 können - wie später ausgeführt - an der oben definierten Subeinheit mittels des Zusammenhanges nach Gleichung Nr. 49 numerisch für verschiedene Verhältnisse 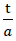 bei n* = 0 bestimmt werden.
bei n* = 0 bestimmt werden.
Wirkliche Schaumgläser verhalten sich in elastischer Hinsicht isotrop; d.h. sie besitzen einen Elastizitätsmodul E und eine Querdehnungszahl ν.
Wie kann man auf Grund der Elastizitätsmoduln cij jdes homogenen - anisotropen Modellschaumglases "TOP" auf die Elastizitätzahlen E und des quasiisotropen Polyederschaumglases schliessen?
Eine Antwort auf diese Frage gibt uns ein Verfahren, das Voigt 1928 vorschlug, um die Elastizitätsmoduln Eund die Querdehnungszahlen eines polykristallinen Aggregates aus den Elastizitätsmoduln cij eines Einkristalles zu finden (14).
Er mittelte die Beziehung zwischen Spannung und gegebener Dehnung aus. Dabei wurde vorausgesetzt, dass der Dehnungszustand gleichförmig durch das Kristallaggregat verlaufe. A priori kann ein beliebiger Materieller Elementarpolyeder unseres Polyederschaumglases wie ein Einkristall behandelt werden.
Aus den Werten c11,c12 und c44 des Modellschaumglases "TOP" erhalten wir mit
56)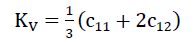
und
57)
Für das quasi-isotrope Polyederschaumglas den Elastizitätsmodul zu
58)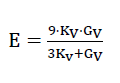
und die Querdehnungszahl
59)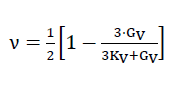
Simultan zur Ermittlung der Bruchfestigkeiten in Richtung z beziehungsweise x oder y des Raumes konnten für verschiedene Belastungsanordnungen die Zusammenhänge zwischen Beanspruchung und Deformation des aus der Umrandung der Subeinheit gebildeten Quaders festgesteilt werden und damit die Elastizitätsmoduln des Modellschaumglases "TOP" c11,c12 und c44 für verschiedene Werte 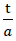 bei jeweils nullgesetztem Porenanteil n∗gewonnen werden. Für andere Werte des Porenanteils n*konnten die dazugehörigen Werte cijproportional umgerechnet werden. Die Elastizitätsmoduln und die Querdehnungszahlen der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt Nr. 1.3.1 zu
bei jeweils nullgesetztem Porenanteil n∗gewonnen werden. Für andere Werte des Porenanteils n*konnten die dazugehörigen Werte cijproportional umgerechnet werden. Die Elastizitätsmoduln und die Querdehnungszahlen der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden dabei gemäss Abschnitt Nr. 1.3.1 zu
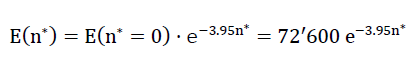
und
ν(n∗)=ν(n∗=0)=0.21
angenommen.
Diese Werte c11,c12 und c44 des homogenen anisotropen Modellschaumglases "TOP" und die aus ihnen nach Voigt bestimmten Elastizitätsmoduln Eund Querdehnungszahlen ν für das quasi-isotrope Polyederschaumglas wurden auch in der Tabelle auf Seite 52 eingetragen. Die Zusammenhänge zwischen der Dichte ρ des quasi-isotropen Polyederschaumglases und seinen Elastizitätsmoduln E und Querdehnungszahlen ν wurden in den Bildern Nr. 33 und Nr. 34 graphisch dargestellt.
Weist der Elastizitätsmodul E(n∗=0) des Glasgrundmaterials der Zellwandfolien nicht den hier für die Berechnung der Tabellenwerte c11,c12,c44,EV und νV und dem Aufzeichnen der Schaubilder für die Elastizitätsmoduln EV und Querdehnungszahlen νV angenommenen Wert 72'600 N/mm2, sondern irgend einen anderen Wert E̅(n∗=0) auf, so müssen die entsprechenden Tabellenwerte und die dazugehörenden Diagramme nur mit dem Korrekturfaktor 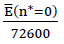 multipliziert werden.
multipliziert werden.
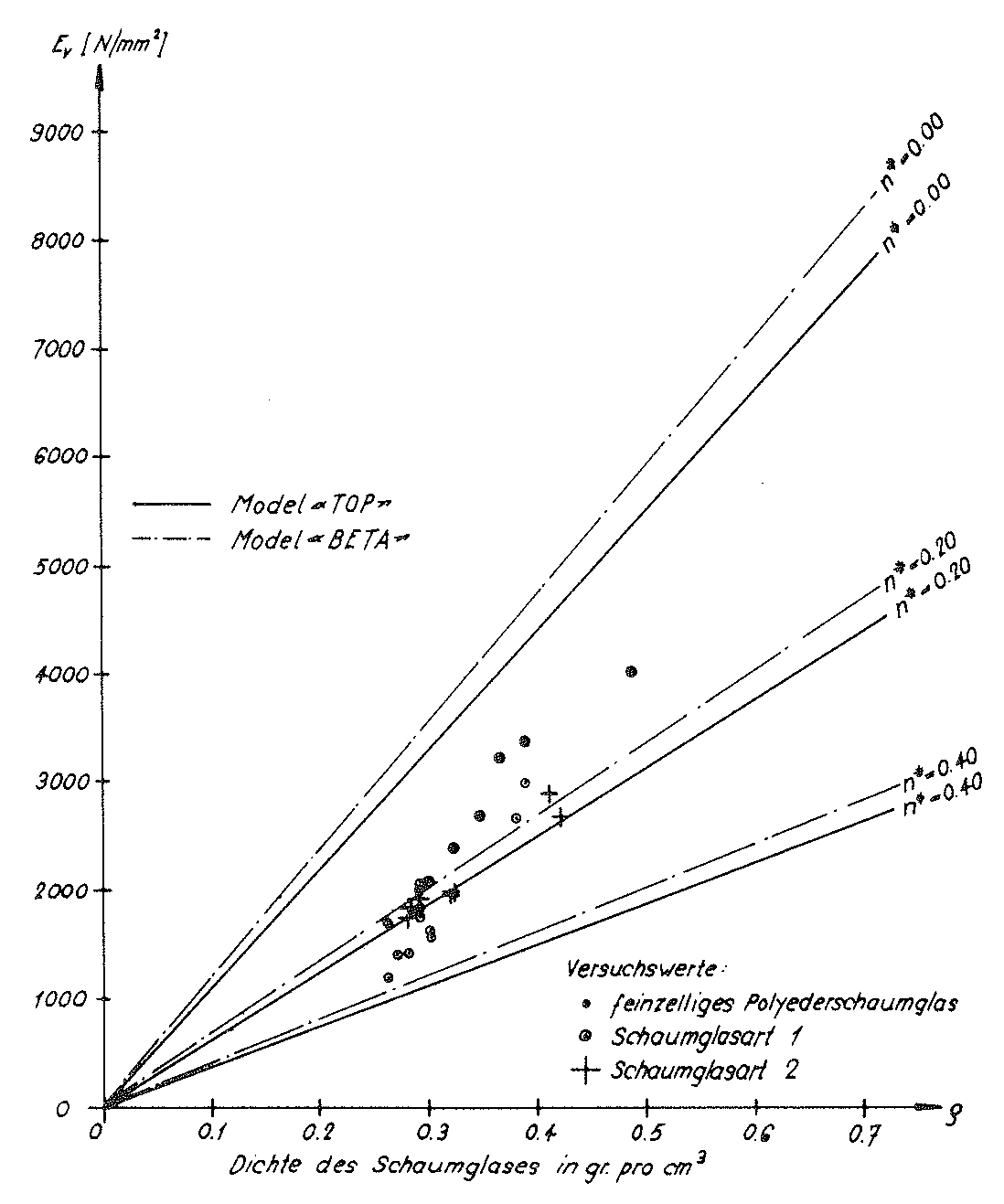
Bild Nr. 33. Der Elastizitätsmodul des Modellschaumglases "TOP"
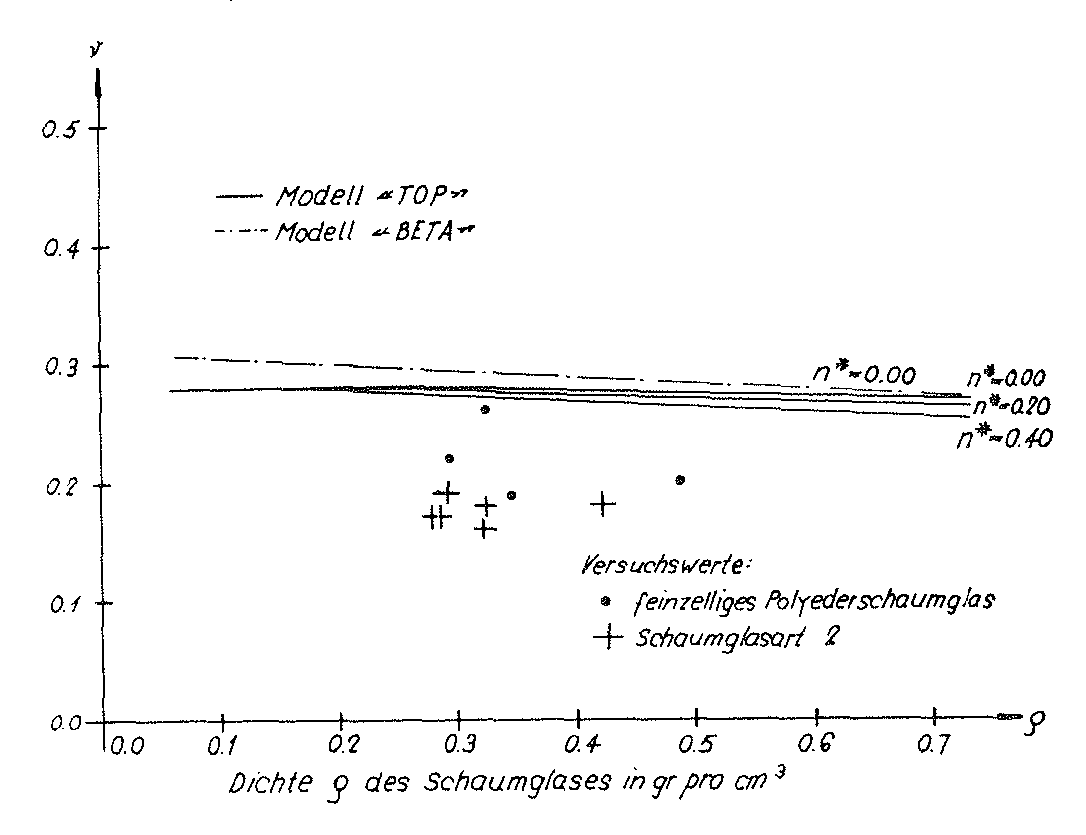
Bild Nr. 34. Die Querdehnungszahl des Modellschaumglases "TOP"
In Abschnitt Nr. 1.4.2. des Kapitels A wurde ein Idealschaumglas erwähnt, dessen Zellwerk aus lauter kongruenten β-Tetrakaidekahedrons als Grundpolyeder gebildet wird! Die prozentuale Verteilung der vier-, fünf- und sechseckigen Teilflächen seines Zellwerkes entspricht ungefähr den Beobachtungen in der Natur.
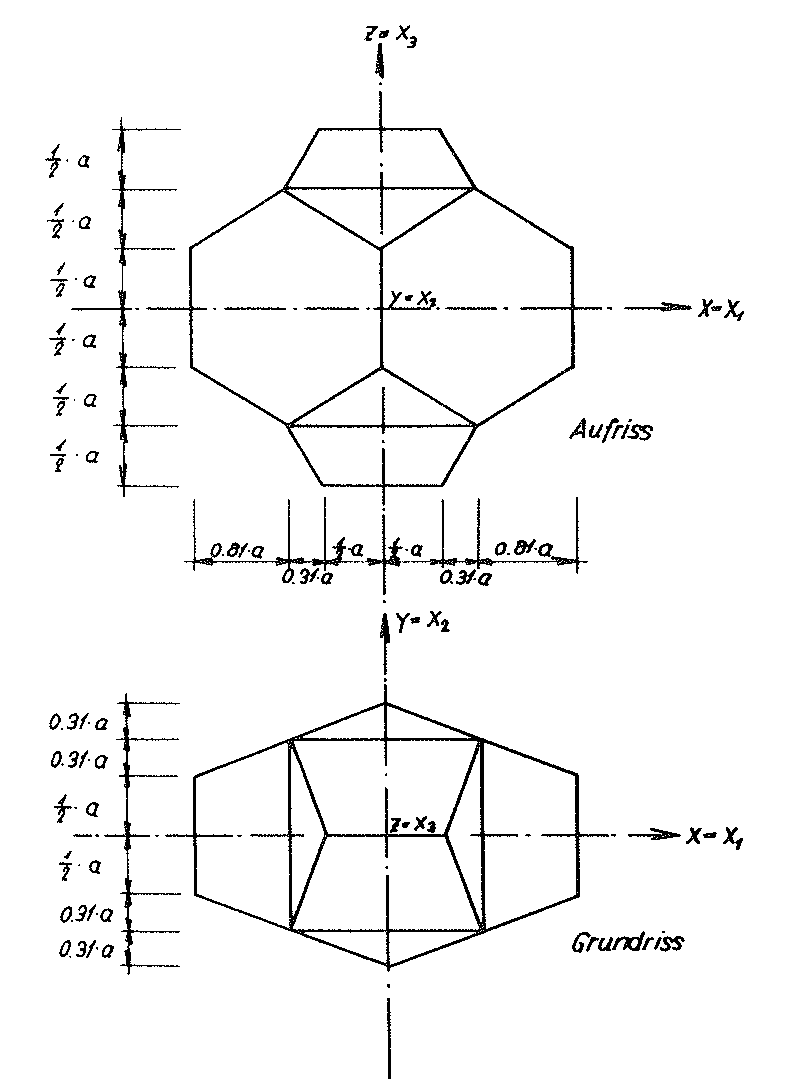
Bild Nr. 35. Grundpolyeder des Modellschaumglases "BETA"
Das β -Tetrakaidekahedron in Bild Nr. 5c kann so "deformiert" werden, dass alle krummlinigen "Kanten" gerade und sämtliche gekrümmten Flächen
(Minimalflächen) eben werden. Bild Nr. 35 zeigt das auf diese Weise gewonnene Polyeder. Es besitzt 22 Flächen, 24 Ecken und 44 Kanten und soll künftig als β - Flächner benannt werden.
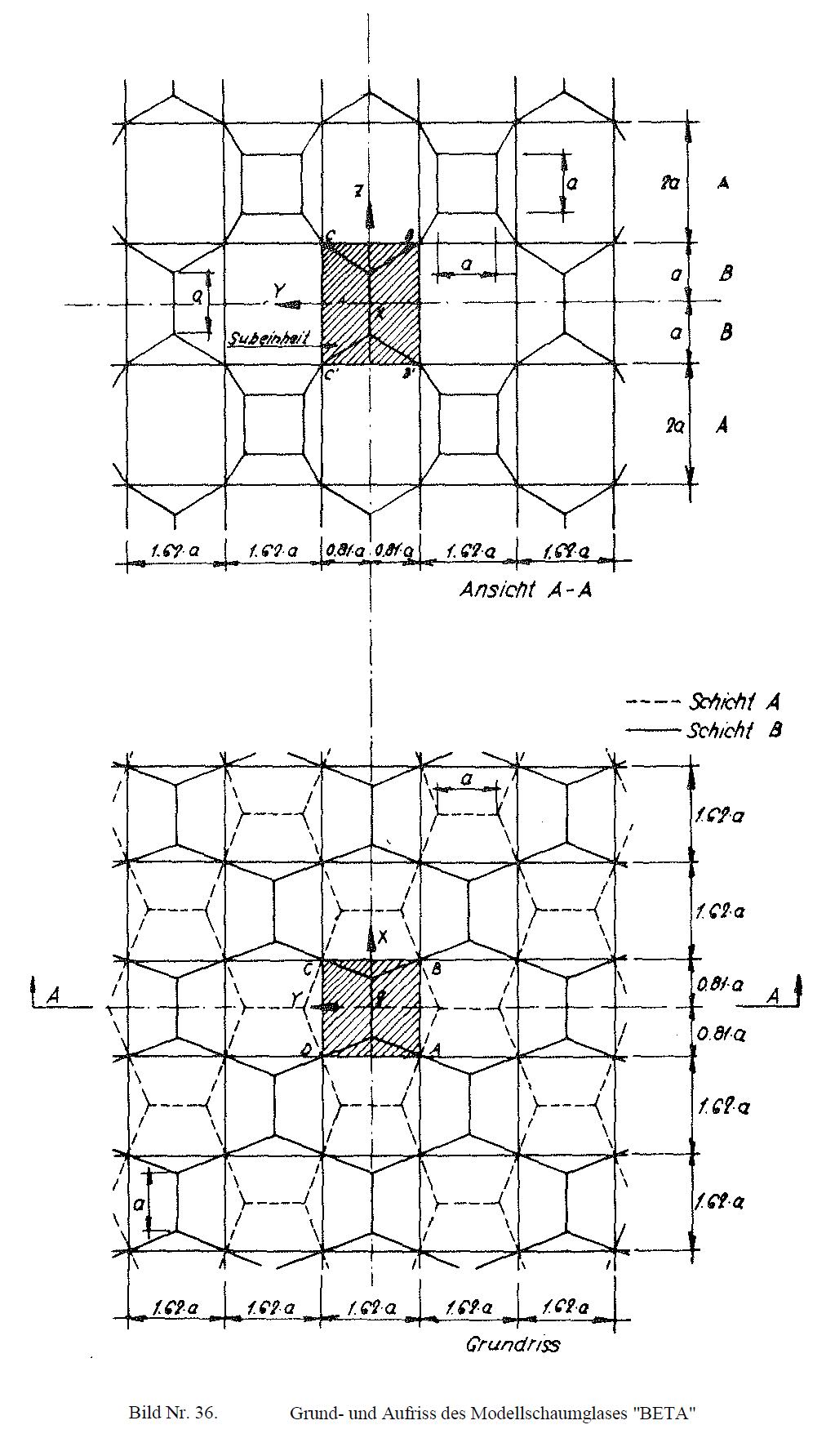
Seine Abmessungen wurden so gewählt, dass er als Elementarpolyeder das raumerfüllende Zellwerk eines Modellpolyederschaumglases aufbauen kann. Bild Nr. 36 zeigt im Grund- und Aufriss das so erhaltene Modellschaumglas "BETA". Der β - Flächner weist folgende Symmetrieelemente auf:
- 1)drei mit den Koordinatenachsen x, y und z zusammenfallende zweizählige Drehachsen;
- 2)die drei durch die Koordinaten x, y und z definierten Symmetrieebenen xy, xz und yz; und
- 3)ein mit dem Schwerpunkt des Polyeders zusammenfallendes Symmetriezentrum.
Diese Symmetrieelemente bilden eine Punktgruppe (Kristallklasse), die mit den international bekannten Symbolen mmm oder 2/mm bezeichnet werden kann. Sie wird dem Orthorhombischen Kristallsystem zugeordnet und gilt natürlich auch für das Zellwerk des allseitig unbegrenzten Körpers aus Modellschaumglas "BETA".
Wie beim Modellschaumglas "TOP" werden auch hier die Plateauränder (siehe Bild Nr. 14) und die Tatsache, dass die Zellwandfolien aus Kugelschaumglas bestehen, berücksichtigt.
Die auf die Volumeneinheit bezogene Mittelfläche der Wandfolien des Modellpolyederschaumglases "BETA" beträgt
60)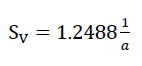
Dabei bedeutet a die Länge, die zur Beschreibung der Grundpolyeder des Zellwerkes, das die Mittelflächen der Zellwandfolien des Modellschaumglases bilden, verwendet wird. Unter Vernachlässigung der Plateauränder mit dem Radius r und der Durchdringung der ebenen Zellwandfolien der Stärke t im Bereiche ihrer gemeinsamen "Schnittlinien" erhält man algebraisch die Komponente des gesamten Porenanteils n = 1- 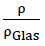 eines Körpers aus dem Modellschaumglas "BETA", die auf die von den Zellwandfolien aus Kugelschaumglas eingeschlossenen polyedrischen Zellblasen entfällt zu
eines Körpers aus dem Modellschaumglas "BETA", die auf die von den Zellwandfolien aus Kugelschaumglas eingeschlossenen polyedrischen Zellblasen entfällt zu
61)nz=n⋅ω=1−SV⋅t
Berücksichtigt man aber noch den Einfluss der kreiszylinderförmig angenommenen Plateauränder mit dem Kreiszylinderradius r (siehe Bild Nr. 14), so ergibt sich der Ausdruck
62)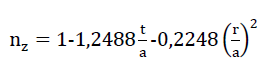
Aus denselben Gründen wie beim Modellschaumglas "TOP" werden auch hier die Radien der kreiszylinderförmigen Plateauränder zu r=2t angenommen. Damit vereinfacht sich die Gleichung Nr. 62 zum Ausdruck
63)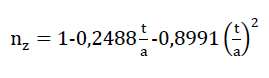
Nach dieser Beziehung und des aus Gleichung Nr. 4 in Kapitel A folgenden Zusammenhanges
64)n=n*+(1-n*)⋅nz
zwischen dem Porenanteil n des Polyederschaumglases und seinen Parametern n* und nz beträgt die Dichte des Modellschaumglases "BETA"
65)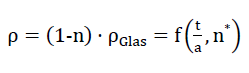
Wie Grund- und Aufriss auf Bild Nr. 36 zeigen, kann das aus den Mittelflächen der Zellwandfolien des Modellschaumglases "BETA" gebildete Zellwerk nicht nur durch seine kongruenten Elementarpolyeder (β - Flächner), sondern auch durch eine gesetzmässige Anordnung von lauter kongruenter Subeinheiten beschrieben werden. Bild Nr. 37 zeigt eine solche Subeinheit!
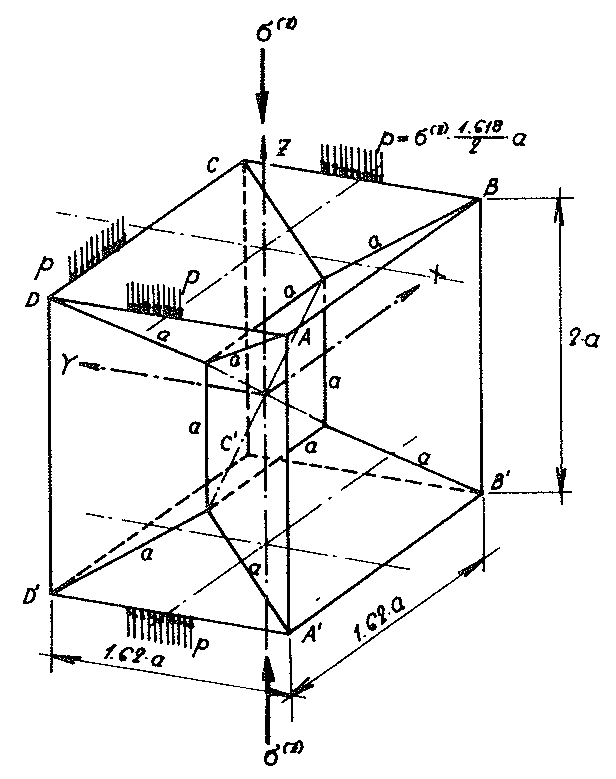
Bild Nr. 37. Subeinheit des Modellschaumglases "BETA"
Der Einfachheit halber soll der allseitig unbegrenzte Modellschaumglaskörper nur durch die in x- und y- Richtung unbegrenzte Flächenlast σ(z) beansprucht werden (siehe Bild Nr. 37)!
Jede aus dem Zellwerk des Modellschaumglases "BETA" gebildete Subeinheit erfährt bei σ(z) als Ganzes eine Starrkörperverschiebung und Formänderungen. Da alle Subeinheiten gleichberechtigt sind, kann jedes mit einer solchen Subeinheit verbundene Koordinatensystem x,y,z als ruhend betrachtet werden. Dann können die obigen Formänderungen als Relativverschiebungen gegenüber dem System x,y,z gedeutet werden.
Ein Beobachter kann feststellen (siehe Bild Nr. 36), dass vor, während und nach Belastung mit σ(z)
- 1)die vertikalen Ränder (z.B.
 ) der Subeinheiten auf zweizähligen Drehachsen liegen und
) der Subeinheiten auf zweizähligen Drehachsen liegen und
- 2)ihre Eckpunkte A, B, C, D beziehungsweise A', B', C', D' je ein Quadrat definieren.
Diese beiden Fakten zeigen auch, wie jeder vertikale Rand der Subeinheit bei der Belastung σ(z) gerade bleibt und sich nur in der durch seine ursprüngliche Lage und dem Ursprung des mit der Subeinheit verbundenen Koordinatensystems x,y,z bestimmten Ebene relativ verschieben kann.
Wie beim Modellpolyederschaumglas "TOP" in Abschnitt Nr. 1.3.2 können die vertikalen Ränder der Subeinheit des Modelles "BETA" (z.B.  ), die ja alle auf zweizähligen Drehachsen liegen, als sogenannte Gelenklinien aufgefasst werden. Sie fallen mit den vertikalen Diagonalen der aus den Mittelflächen der vertikalen hexagonförmigen Zellwandfolien gebildeten regulären Hexagone zusammen. Somit werden bei der äusseren Flächenbelastung σ(z) die vertikalen Ränder (z.B.
), die ja alle auf zweizähligen Drehachsen liegen, als sogenannte Gelenklinien aufgefasst werden. Sie fallen mit den vertikalen Diagonalen der aus den Mittelflächen der vertikalen hexagonförmigen Zellwandfolien gebildeten regulären Hexagone zusammen. Somit werden bei der äusseren Flächenbelastung σ(z) die vertikalen Ränder (z.B.  ) der dazugehörenden Materiellen Subeinheit - siehe Bild Nr. 37 - pro Längeneinheit nur durch die variablen Normalkräfte nξ und die variablen Drillmomente mξη und Scherkräfte qξ beansprucht, während die Biegemomente mξ verschwinden1).
) der dazugehörenden Materiellen Subeinheit - siehe Bild Nr. 37 - pro Längeneinheit nur durch die variablen Normalkräfte nξ und die variablen Drillmomente mξη und Scherkräfte qξ beansprucht, während die Biegemomente mξ verschwinden1).
Für die weiteren Betrachtungen wird die sinnvolle Annahme getroffen, dass die Kanten der Subeinheit, welche die Seiten der Quadrate ABCD und A'B'C'D' bilden, auf Gelenkgeraden lägen! Infolge dieser willkürlichen Annahme, die mit der Wirklichkeit nicht genau übereinstimmt, können an den horizontalen Rändern der dazugehörenden Materiellen Subeinheit (z.B. ) nur variable Normalkräfte n̅ξ, variable Drillmomente m̅ξη und Scherkräfte q̅ξ angreifen (siehe Bild Nr. 38).
) nur variable Normalkräfte n̅ξ, variable Drillmomente m̅ξη und Scherkräfte q̅ξ angreifen (siehe Bild Nr. 38).
Nach dem soeben Gesagten können somit alle horizontalen und vertikalen Ränder der Materiellen Subeinheit des Modellschaumglases "BETA" wie beim Modell "TOP" mit fiktiven Randträgern (EF=0,GJP=0,EJ=∞) verstärkt werden2), ohne dass irgendwelche Zwängungen entstehen. Bei den horizontalen fiktiven Randträgern trifft dies natürlich nur näherungsweise zu. Schneidet man in Gedanken eine solche verstärkte Materielle Subeinheit aus dem Modellschaumglas "BETA", so erzwingen diese Randträger - wie beim Modell "TOP" - ihre geometrische Verträglichkeit mit den übrigen verstärkten Materiellen Subeinheiten des Schaumglases, wobei die Spannungs-und Verformungszustände in der Materiellen Subeinheit nicht beeinflusst werden.
- 1)Gleiche Ueberlegungen wie beim Modell "TOP"
- 2)Diese vertikalen Randträger besitzen in Bezug auf das mit der Subeinheit verbundene Koordinatensystem x,y,z a priori nur einen Freiheitsgrad.
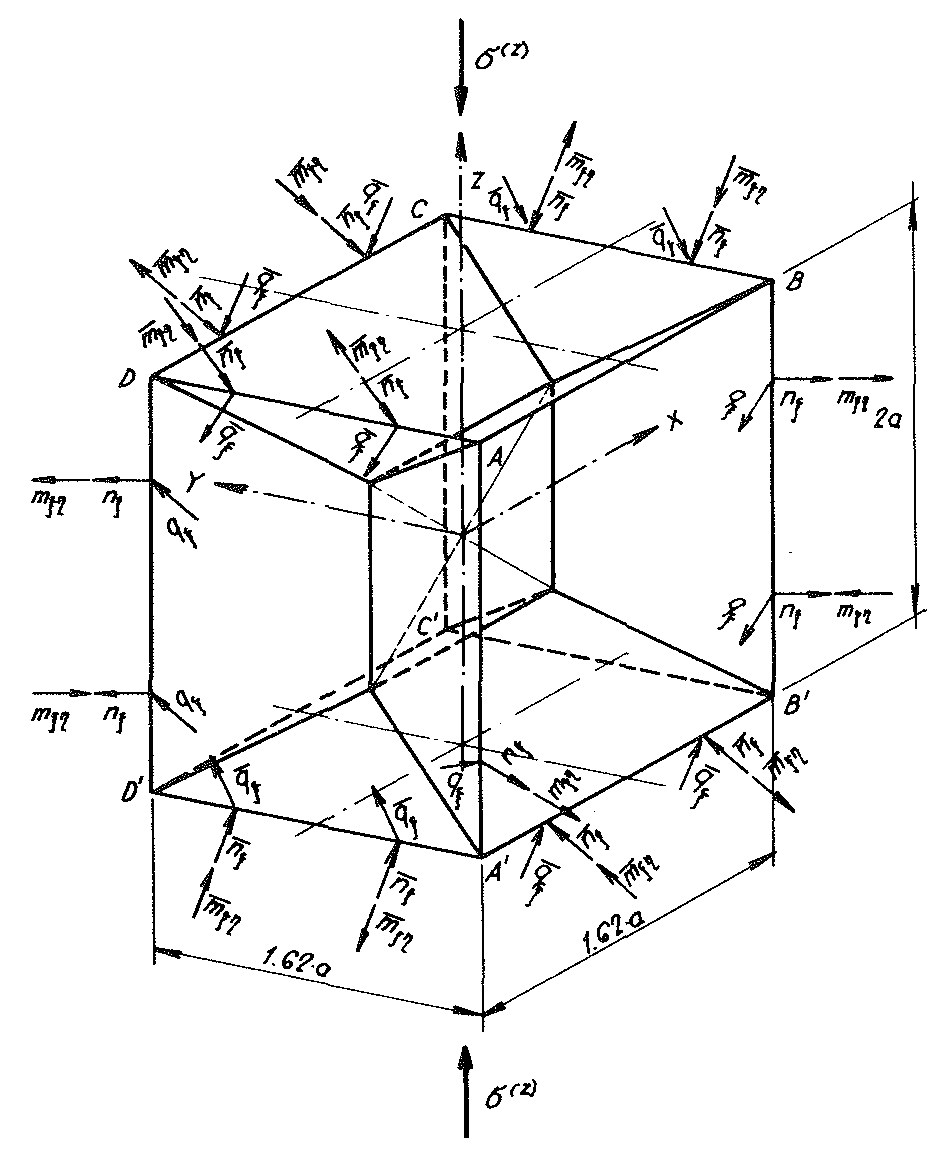
Bild Nr. 38. Die auf die Materielle Subeinheit des Modellschaumglases "BETA" wirkenden Schnittkräfte unter der äusseren Belastung σ(z)
Analog wie beim Modell "TOP" müssen dann für die Ermittlung der Spannungen in der verstärkten Materiellen Subeinheit nur die an ihren horizontalen Rändern (z.B.  ) angreifenden vertikalen Linienlasten
) angreifenden vertikalen Linienlasten
66)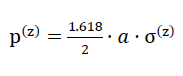
berücksichtigt werden.
Im Einklang mit der Oberflächenhypothese in Abschnitt Nr. 1.3.1 dieses Kapitels kann σ(z) dann der Druckfestigkeit 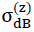 oder der Zugfestigkeit
oder der Zugfestigkeit 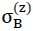 des Modellschaumglases "BETA" gleichgesetzt werden, sobald die grösste Hauptzugspannung an irgend einer Stelle der inneren Oberfläche seiner Polyederblasen die Bruchfestigkeit σB(n∗) seiner als Kontinuum aufgefassten Zellwandfolien aus Kugelschaumglas erreicht. Deshalb sollen zur Ermittlung der Bruchfestigkeiten
des Modellschaumglases "BETA" gleichgesetzt werden, sobald die grösste Hauptzugspannung an irgend einer Stelle der inneren Oberfläche seiner Polyederblasen die Bruchfestigkeit σB(n∗) seiner als Kontinuum aufgefassten Zellwandfolien aus Kugelschaumglas erreicht. Deshalb sollen zur Ermittlung der Bruchfestigkeiten 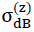 und
und 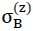 die Spannungszustände auf den Oberflächen der Zellwandungen genau bekannt sein. Die dazu erforderlichen Spannungsanalysen konnten unter Ausnutzung der Symmetrien auf ein "Achtel" der verstärkten Materiellen Subeinheit beschränkt werden. Dieser wurde für die numerischen Spannungsnachweise in 528 finite Elemente aufgeteilt und in Bild Nr. 39 dargestellt.
die Spannungszustände auf den Oberflächen der Zellwandungen genau bekannt sein. Die dazu erforderlichen Spannungsanalysen konnten unter Ausnutzung der Symmetrien auf ein "Achtel" der verstärkten Materiellen Subeinheit beschränkt werden. Dieser wurde für die numerischen Spannungsnachweise in 528 finite Elemente aufgeteilt und in Bild Nr. 39 dargestellt.
Wie die Gleichungen Nr. 1, Nr. 26 und Nr. 63 beweisen, hängt das Verhältnis 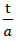 zwischen der Stärke t und der Länge a, welche die Grundpolyeder des Modellschaumglases "BETA beschreibt, nur von seiner Dichte ρ und vom Porenanteil n∗ seiner Zellwandfolien aus Kugelschaumglas alleine ab. Dieses Verhältnis
zwischen der Stärke t und der Länge a, welche die Grundpolyeder des Modellschaumglases "BETA beschreibt, nur von seiner Dichte ρ und vom Porenanteil n∗ seiner Zellwandfolien aus Kugelschaumglas alleine ab. Dieses Verhältnis 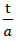 beeinflusst aber den Anteil der Biegenebenspannungen auf den Oberflächen der Zellwandfolien entscheidend, indem bei kleinem
beeinflusst aber den Anteil der Biegenebenspannungen auf den Oberflächen der Zellwandfolien entscheidend, indem bei kleinem 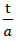 der Membranspannungszustand vorherrscht und bei grossem
der Membranspannungszustand vorherrscht und bei grossem 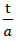 die Biegewirkung sich sehr stark bemerkbar macht (siehe Diagramm auf Bild Nr. 48). Aus diesen Gründen kann auf die massgebende Beeinflussung des Bruchverhaltens des Modellpolyederschaumglases "BETA" durch das Verhältnis
die Biegewirkung sich sehr stark bemerkbar macht (siehe Diagramm auf Bild Nr. 48). Aus diesen Gründen kann auf die massgebende Beeinflussung des Bruchverhaltens des Modellpolyederschaumglases "BETA" durch das Verhältnis 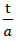 =f (ρ,n∗) und die Zugfestigkeit
=f (ρ,n∗) und die Zugfestigkeit 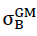 (n∗ = 0) des Glasgrundmaterials der Zellwandfolien aus Kugelschaumglas (Oberflächenhypothese) geschlossen werden. Für die Ausführung der numerischen Spannungsanalysen, welche die Grundlagen der Prognosen der Bruchfestigkeiten des Modellpolyederschaumglases "BETA" bilden, brauchte nach dem weiter oben Gesagten nur das Verhältnis
(n∗ = 0) des Glasgrundmaterials der Zellwandfolien aus Kugelschaumglas (Oberflächenhypothese) geschlossen werden. Für die Ausführung der numerischen Spannungsanalysen, welche die Grundlagen der Prognosen der Bruchfestigkeiten des Modellpolyederschaumglases "BETA" bilden, brauchte nach dem weiter oben Gesagten nur das Verhältnis  =f (ρ,n∗) bei Nullsetzen des Parameters n∗ variiert zu werden, da die entsprechenden Werte für andere n∗≠0 wegen der Oberflächenhypothese proportional umgerechnet werden können.
=f (ρ,n∗) bei Nullsetzen des Parameters n∗ variiert zu werden, da die entsprechenden Werte für andere n∗≠0 wegen der Oberflächenhypothese proportional umgerechnet werden können.
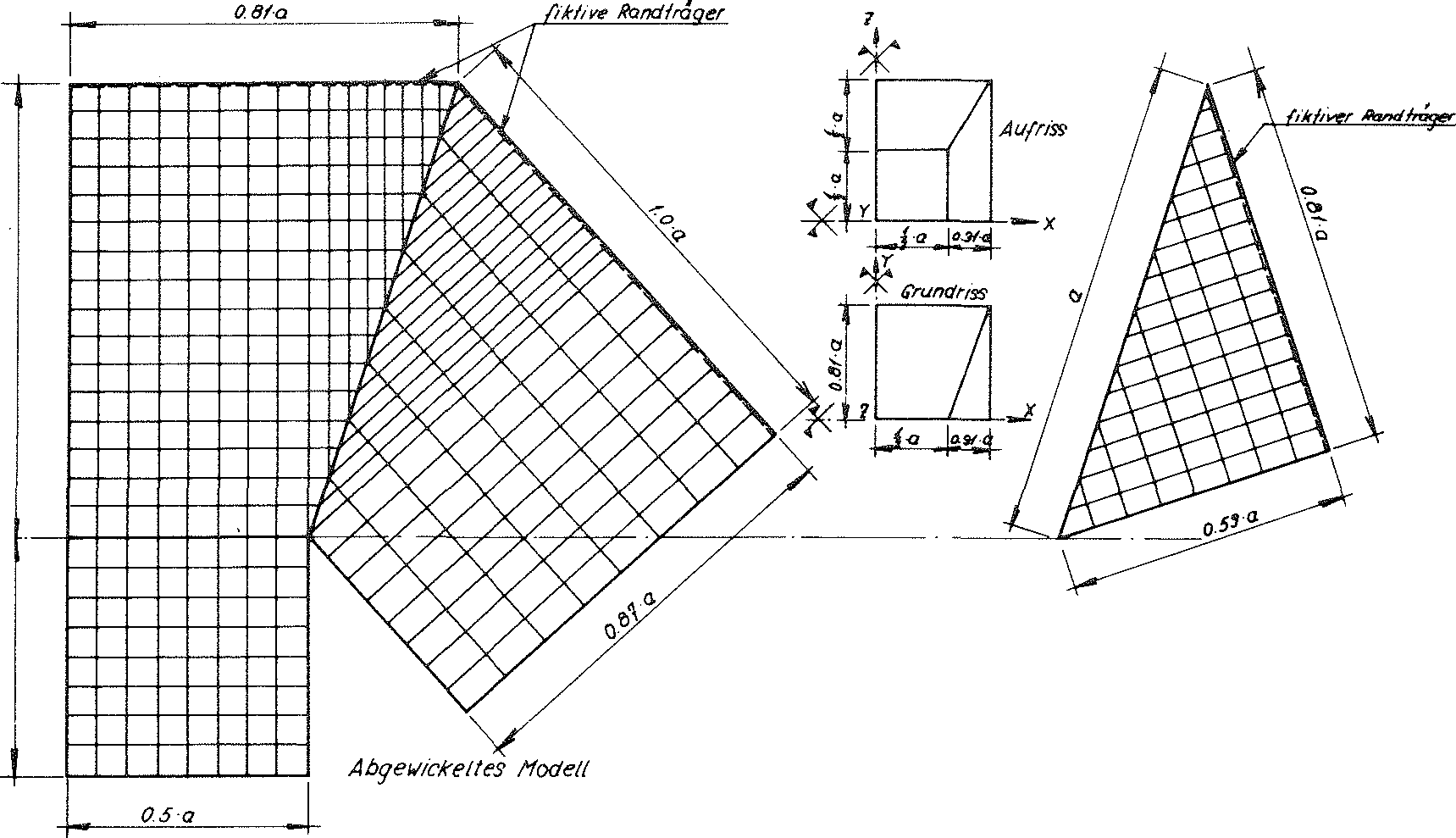
Bild Nr. 39. Aufteilung der durch Ausnützung der Symmetrien reduzierten verstärkten Materiellen Subeinheit des Modellschaumglases "BETA" in 528 finite Elemente
Die Zugfestigkeiten, die Elastizitätsmoduln und die Querdehnungszahlen der als Kontinuum betrachteten Zellwandfolien aus Kugelschaumglas wurden gemäss Abschnitt Nr. 1.3.1 zu
67)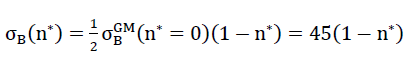
68)E(n∗)=E(n∗=0)⋅𝚎−3.95n∗=72′600⋅𝚎−3.95n∗
und
69)ν(n∗)=ν(n∗=0)=0.21
angenommen.
In der Tabelle auf Seite Nr. 79 wurden die Rechenergebnisse zusammengestellt. Bild Nr. 40 zeigt als Schaubild die Ergebnisse dieser Berechnungen. Es zeigt sich dabei, dass die Dichte ρ des Modellschaumglases einen massgebenden Einfluss auf die Bruchfestigkeiten  und
und 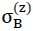 ausübt, wohingegen dies in Bezug auf den Porenanteil n∗ der Zellwandfolien aus Kugelschaumglas nicht mehr so deutlich gesagt werden kann.
ausübt, wohingegen dies in Bezug auf den Porenanteil n∗ der Zellwandfolien aus Kugelschaumglas nicht mehr so deutlich gesagt werden kann.
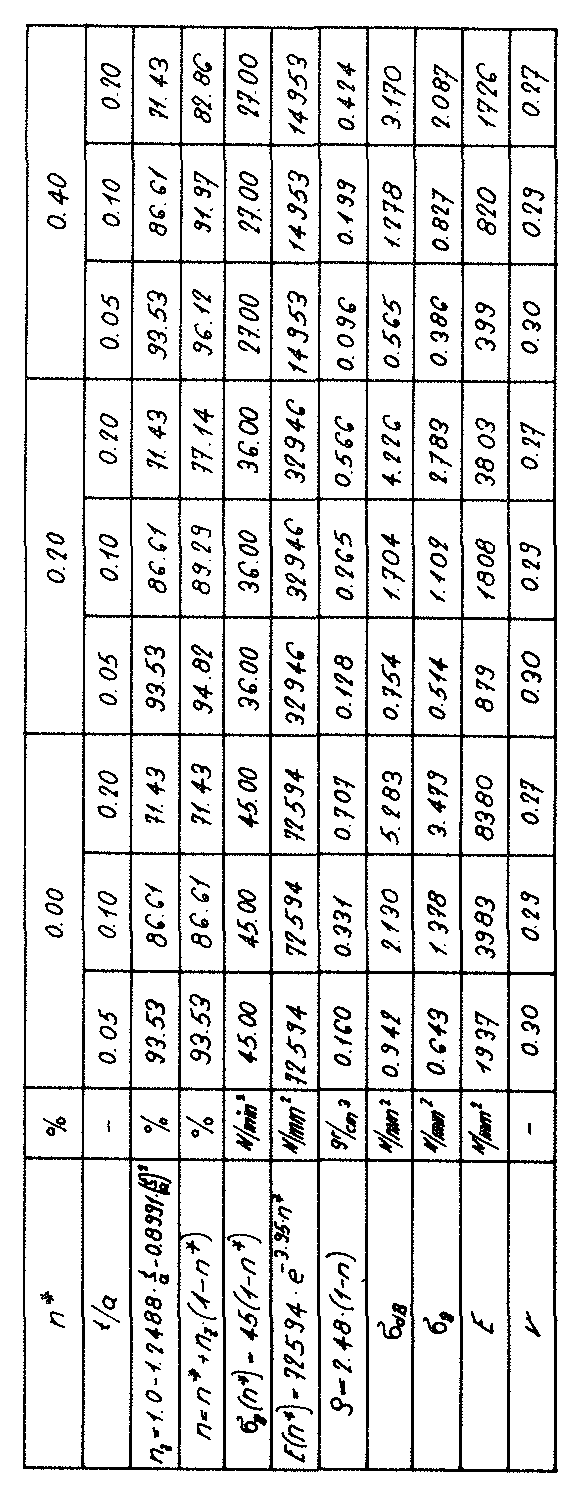
Bild Nr. 40.
Wie bereits in Abschnitt Nr. 1.3.3.1. gesagt, bilden die Symmetrieelemente des Modellschaumglases "BETA" die Punktgruppe (Kristallklasse) mmm oder 2/mm. Folglich weist die symmetrische Matrix (cij) der Elastizitätsmoduln cij nach dem Neumann'schen Prinzip (siehe Abschnitt Nr. 1.3.2.2.4.) folgende Struktur auf:
71)
Grund- und Aufriss des Zellwerkes des Modellschaumglases "BETA" auf Bild Nr. 36 zeigen eine Schichtstruktur (ABABA ...); In Richtung z wechselt immer eine Schicht A von β -Flächner, deren x1-Achsen (siehe Bild Nr. 35) in Richtung x des Raumes ausgerichtet sind, mit einer Schicht B von β -Flächner, deren x1- Achsen in Richtung y des Raumes weisen, ab.
Als Konsequenz der soeben beschriebenen Morphologie seines Zellwerkes können beim Modellschaumglas "BETA" bezüglich den Richtungen x und y des Raumes nur gleiche mechanische Verhaltensweisen erwartet werden. Auf Grund dieser Tatsache bestehen zwischen den Elementen cij der Matrix (cij) die Beziehungen
c11=c12;c13=c23 und c44=c55 .
Die Matrix der Elastizitätsmoduln cij weist dann folgende vereinfachte Struktur auf
72)
Ein Einkristall, dessen Symmetrieelemente die Punktgruppe oder Kristallklasse 4/mmm bilden, besitzt eine Matrix (cij), welche die gleiche Elementenstruktur aufweist!
Trotz der Tatsache, dass die Elastizität des Modellschaumglases "BETA" nur durch die sechs Elastizitätsmoduln
c11,c33,c44,c66,c12 und c13
genau beschrieben werden kann, wurden zwecks unserer groben Abschätzungen nur die unter der äusseren Belastung σ(z)=−σ3 auftretenden Grössen
73)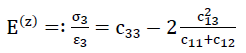
74)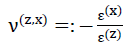 und
und
75)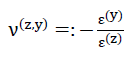
rechnerisch bestimmt.
Dabei gelten folgende Gleichheiten:
- 1)σ3=−σ(z)
- 2)ε3=ε(z)
- 3)ε(x)=ε(y)=ε1=εz
- 4)ν(z,x)=ν(z,y)
In den folgenden Ausführungen sollen die Werte E(z) und ν(z,x) = ν(z,y) als Elastizitätsmodul beziehungsweise als Querdehnungszahl des Modellschaumglases bezeichnet werden!
In der Tabelle auf Seite 79 wurden auch die simultan mit den Bruchfestigkeiten an der verstärkten Materiellen Subeinheit bestimmten Werte E(z) und ν(z,x)=ν(z,y) eingetragen. Die Bilder Nr. 41 und Nr. 42 zeigen die Graphen E(z)(ρ,n∗) beziehungsweise ν(z,x)(ρ,n∗)=ν(z,y)(ρ,n∗) für die Parameter n∗=0.00, n∗=0.20 und n∗=0.40.
In den für das Modell "TOP" geltenden Diagrammen auf den Bildern Nr. 26, 27, 33 und Nr. 34 wurden auch die Graphen 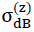 (ρ,n∗=0),
(ρ,n∗=0), 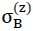 (ρ,n∗=0), E(z)(ρ,n∗) und ν(z,x)(ρ,n∗=0)=ν(z,y)(ρ,n∗=0) des Modellpolyederschaumglases "BETA" eingetragen.
(ρ,n∗=0), E(z)(ρ,n∗) und ν(z,x)(ρ,n∗=0)=ν(z,y)(ρ,n∗=0) des Modellpolyederschaumglases "BETA" eingetragen.
Obwohl das Modellschaumglas "BETA" nur für eine äussere Flächenbelastung σ(z) in Richtung z des Raumes untersucht wurde, zeigen die soeben erwähnten Schaubilder, dass sich die Voraussagen der beiden Modelle "TOP" und "BETA" in Bezug auf die mechanischen Eigenschaften nicht wesentlich unterscheiden. Deshalb soll für die künftigen theoretischen Untersuchungen nur das Modellschaumglas "TOP" verwendet werden.
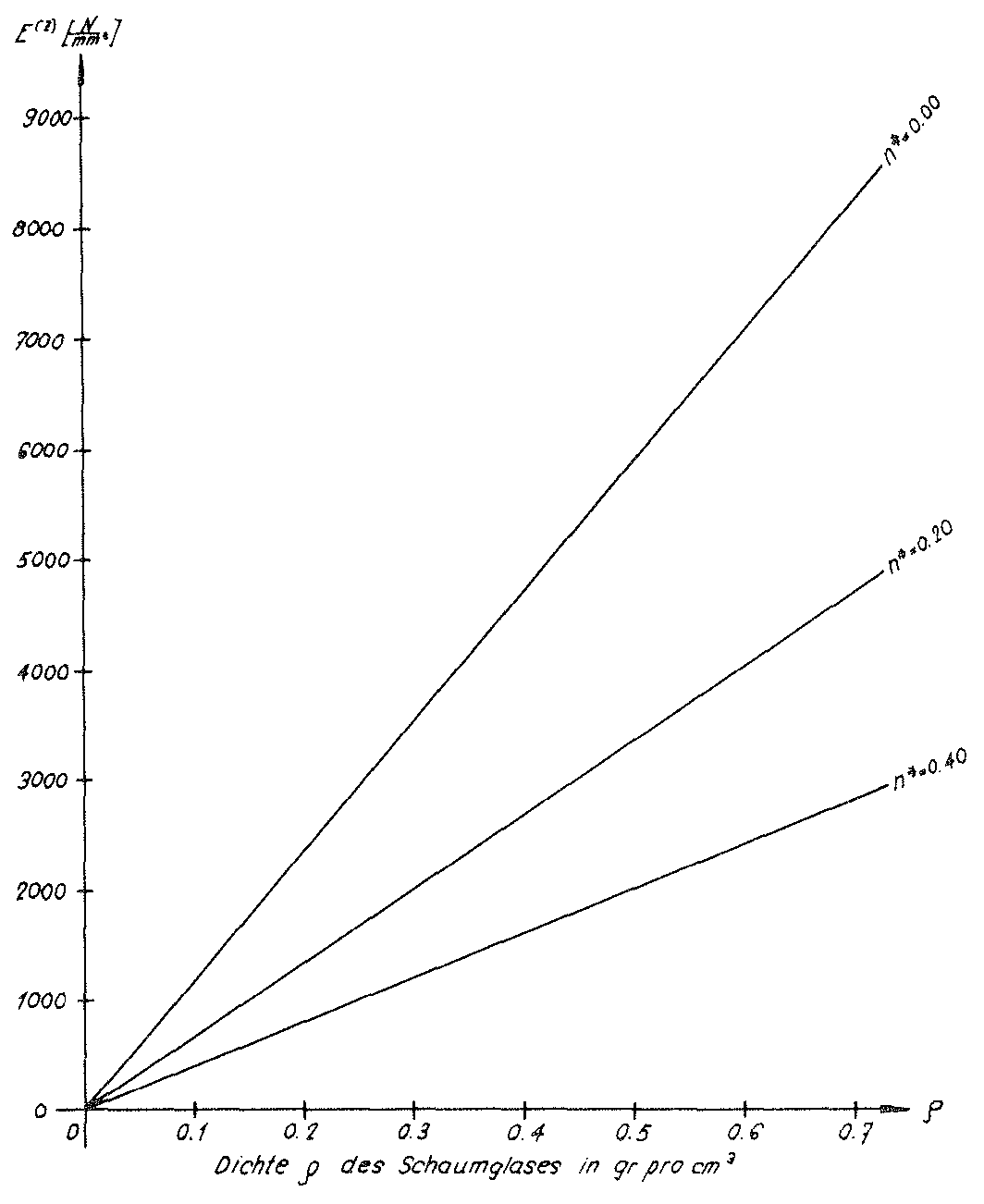
Bild Nr. 41. Der Elastizitätsmodul des Modellschaumglases "BETA"
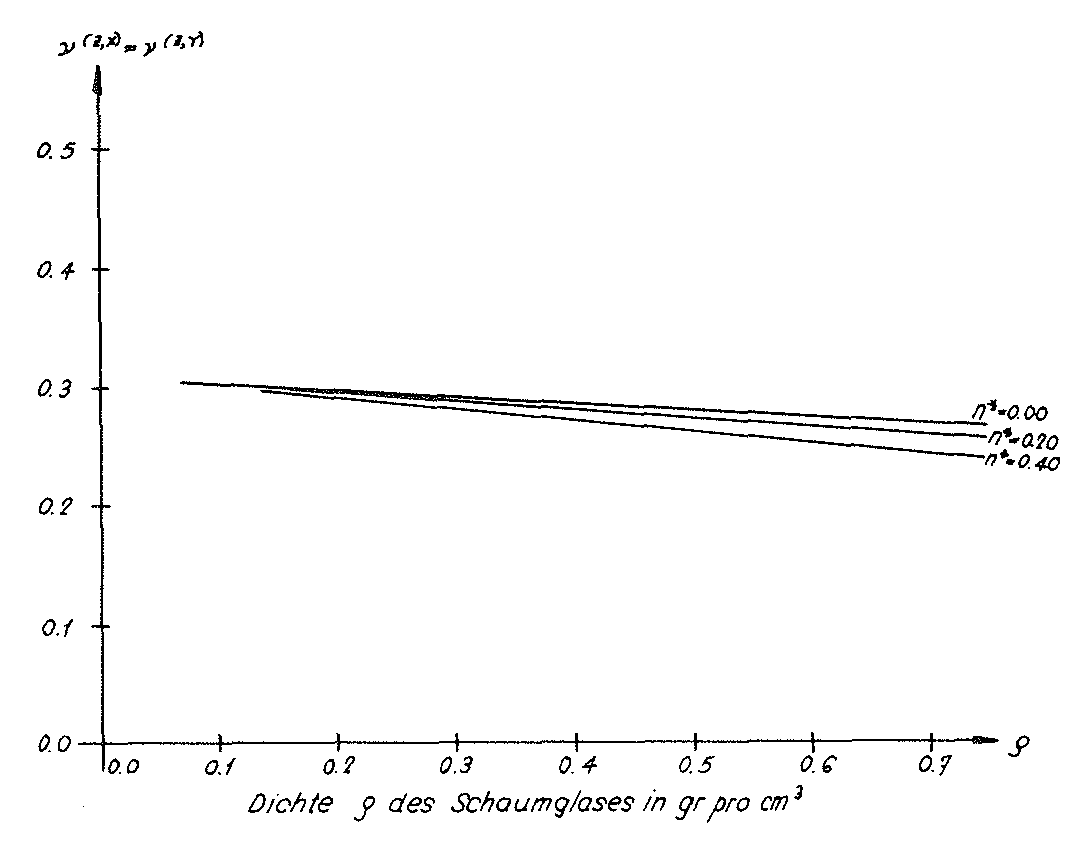
Bild Nr. 42. Querdehnungszahl des Modellschaumglases “BETA“
Die bisher betrachteten Modellpolyederschaumgläser "TOP" und "BETA" sind anisotrop! Im Hinblick auf die Möglichkeit, Schaumglasziegel im Strangpressverfahren zu erzeugen, wollen wir ein neues ideelles Polyederschaumglas betrachten, das eine betonte "Orthotropie" aufweist1). Am einfachsten kann das Zellwerk eines solchen Modellschaumglases durch die affine Transformation des Zellwerkes des Modellschaumglases "TOP" in Richtung z des Raumes (siehe Bild Nr. 11) gewonnen werden2),
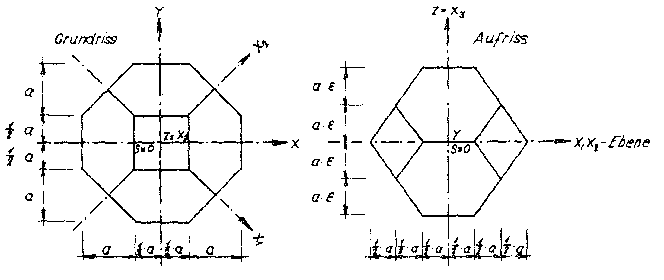
Bild Nr. 43. Grundpolyeder des Modellschaumglases "ORTHO"
Bild Nr. 43 zeigt in Grund- und Aufriss den Elementarpolyeder des Zellwerkes des so erhaltenen neuen Polyederschaumglases, das kurz "Modellschaumglas "ORTHO” genannt werden soll. Dieser Grundpolyeder ist eine Kombination der Formen: Tetragonale Dipyramide, Tetragonales Prisma und Basisbinakoid.
Da es sich eigentlich um eine Tetragonale Dipyramide mit abgeschnittenen Ecken handelt, wollen wir sie künftig als "Abgeschnittene Tetragonale Dipyramide" bezeichnen!
- 1)Das Wort "Orthotropie" ist ein Synonym für "Orthogonale Anisotropie".
- 2)Kristallographisch: "Homogene Verzerrung entlang z-Achse".
Dieses Polyeder weist folgende Symmetrieelemente auf:
- 1)eine mit der z-Achse (=x3-Achse) zusammenfallende vierzählige Drehachse;
- 2)zwei auf den Koordinatenachsen x und y liegende zweizählige Drehachsen;
- 3)zwei durch die x1- und x2- Achsen definierte zweizählige Drehachsen;
- 4)fünf Symmetrieebenen, von welchen jede eine der obigen Drehachsen rechtwinklig im Schwerpunkt S des Grundpolyeders schneidet; und
- 5)ein Symmetriezentrum.
Diese Symmetrieelemente bilden eine Punktgruppe, die mit dem allgemein gebräuchlichen Symbol 4/mmm bezeichnet und zum tetragonalen Kristallsystem zugeordnet wird. Diese Punktgruppe 4/mmm gilt natürlich auch für den allseitig unbegrenzten Körper aus Modellschaumglas "ORTHO".
Weil das Zellwerk des Modellschaumglases "TOP" infolge obiger affiner Transformation nur ein Sonderfall des neuen Modelles bildet, können Grund-und Aufriss auf Bild Nr. 11 auch für die graphische Darstellung des Modellschaumglases "ORTHO" verwendet werden.
Die Geometrie des Zellwerkes des Modellschaumglases "ORTHO" steht im Widerspruch zu den Prinzipien von J. Plateau (siehe Kapitel A, Abschnitt 1.2.)! Die auf die Volumeneinheit bezogene Mittelfläche der Wandfolien des Modellschaumglases "ORTHO" beträgt
76)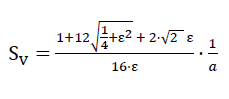
Die Parameter a und ε auf der rechten Seite dieser Gleichung wurden auf Bild Nr. 43 eingetragen!
Bezüglich den weiteren Untersuchungen werden die Plateauränder (siehe Bild Nr. 14) vernachlässigt und die ebenen Zellwandfolien der konstanten Stärke t des Modellpolyederschaumglases als aus kompakten Glasgrundmaterial bestehend angenommen (d.h. n∗=0).
Unter Vernachlässigung des Einflusses der Durchdringung je dreier ebenen Zellwandfolien der Stärke t im Bereiche ihrer gemeinsamen "Schnittlinie"
beträgt der gesamte Porenanteil des Modellpolyederschaumglases "ORTHO"
77)n=1−Sv⋅t
Damit nimmt nach Gleichung Nr. 1 die Dichte des Schaumglases den Wert
78)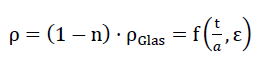
Wie beim Modellschaumglas "TOP" kann das Zellwerk des Modellschaumglases "ORTHO" auch durch die periodische Anordnung von lauter kongruenter "Subeinheiten" gewonnen werden.
Eine solche Subeinheit zeigt Bild Nr. 44.
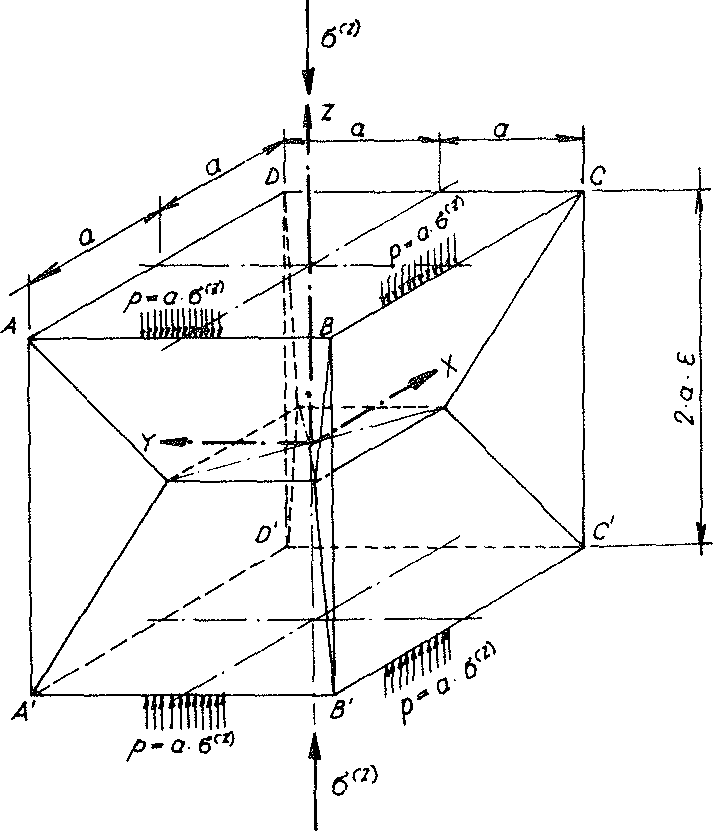
Bild Nr. 44. Subeinheit des Modellpolyederschaumglases "ORTHO"
Ein Betrachter des Bildes Nr. 11 kann feststellen, dass die Zweizähligkeit der Drehachsen, auf denen sämtliche horizontalen und vertikalen Ränder (z.B.  ) der betrachteten Subeinheit liegen, durch die affine Transformation in Richtung der z-Achse (Vierzählige Drehachse) erhalten bleibt.
) der betrachteten Subeinheit liegen, durch die affine Transformation in Richtung der z-Achse (Vierzählige Drehachse) erhalten bleibt.
Hier soll nur die auf das Schaumglas wirkende in x- und y- Richtung unbegrenzte Flächenlast σ(z) betrachtet werden! Wie ein Vergleich mit Abschnitt Nr. 1.3.2. zeigt, werden dann die geometrischen Randbedingungen (Verträglichkeitsbedingungen) an sämtlichen horizontalen und vertikalen Kanten der Subeinheiten des Zellwerkes des Modellschaumglases "TOP" durch die affine Transformation, die zum Zellwerk des Modellschaumglases "ORTHO" führt, nicht verändert. Daher gelten für die Ränder der Subeinheiten des Modellschaumglases "ORTHO" dieselben geometrischen Randbedingungen wie für die Subeinheiten des Modellschaumglases "TOP". Deshalb können alle Materiellen Subeinheiten des Modellschaumglases "ORTHO" auf die genau gleiche Art wie beim Modell "TOP" durch das Anbringen von fiktiven Randträgern verstärkt werden. Diese Verstärkungen verursachen keine zusätzlichen Zwängungen im Modellschaumglas. Schneidet man gedanklich eine solche verstärkte Materielle Subeinheit aus dem Modellschaumglas "ORTHO", so erzwingen diese Randträger ihre geometrische Verträglichkeit mit den übrigen verstärkten Materiellen Subeinheiten des Schaumglases, wobei die Spannungs- und Verformungszustände in der Materiellen Subeinheit nicht beeinflusst werden.
Analog wie beim Modell "TOP" müssen dann für die Ermittlung der Spannungen in der verstärkten Materiellen Subeinheit nur die an ihren horizontalen Rändern angreifenden vertikalen Linienlaste
79)p(z)=а⋅σ(z)
berücksichtig werden (siehe Bild Nr. 44).
In Uebereinstimmung mit der Oberflächenhypothese in Abnschnitt Nr. 1.3.1 erreicht σ(z) dann die Druckfestigkeit 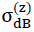 oder die Zugfestigkeit
oder die Zugfestigkeit 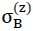 des Modellpolyederschaumglases "ORTHO", sobald die grösste Hauptzugspannung auf der Oberfläche irgend einer seiner Zellwandfolien den Wert σB(n∗=0) annimmt. Darum sollen die Randspannungszustände der Zellwandfolien möglichst genau bekannt sein!
des Modellpolyederschaumglases "ORTHO", sobald die grösste Hauptzugspannung auf der Oberfläche irgend einer seiner Zellwandfolien den Wert σB(n∗=0) annimmt. Darum sollen die Randspannungszustände der Zellwandfolien möglichst genau bekannt sein!
Zu den notwendigen numerischen Spannungsberechnungen wurde die verstärkte
Materielle Subeinheit unter Benutzung verschiedener Symmetrieebenen auf ein "Sechzehntel" beschränkt. Dieser "Sechzehntel" besteht aus 340 finiten Elementen und wurde für den Spezialfall 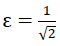 auf Bild Nr. 25 zeichnerisch festgehalten.
auf Bild Nr. 25 zeichnerisch festgehalten.
Nach Gleichung Nr. 78 hängt das Verhältnis 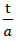 zwischen der Stärke t und der die Grundpolyeder des Zellwerkes des Modellpolyederschaumglases "ORTHO" beschreibende Länge a nur von seiner Dichte ρ und dem Parameter ε ab. Dieses Verhältnis
zwischen der Stärke t und der die Grundpolyeder des Zellwerkes des Modellpolyederschaumglases "ORTHO" beschreibende Länge a nur von seiner Dichte ρ und dem Parameter ε ab. Dieses Verhältnis 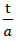 beeinflusst aber den Anteil der Biegenebenspannungen auf den Oberflächen der Zellwandfolien entscheidend, indem bei kleinem
beeinflusst aber den Anteil der Biegenebenspannungen auf den Oberflächen der Zellwandfolien entscheidend, indem bei kleinem 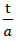 der Membranspannungszustand vorherrscht und bei grossem
der Membranspannungszustand vorherrscht und bei grossem 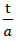 die Biegewirkung sich sehr stark bemerkbar macht. Aus diesen Gründen kann geschlossen werden, dass das Bruchverhalten des Modellpolyederschaumglases "ORTHO" neben dem Verhältnis
die Biegewirkung sich sehr stark bemerkbar macht. Aus diesen Gründen kann geschlossen werden, dass das Bruchverhalten des Modellpolyederschaumglases "ORTHO" neben dem Verhältnis 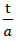 = f (ρ,ε)auch von der Zugfestigkeit
= f (ρ,ε)auch von der Zugfestigkeit 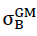 (n∗=0) des Glasgrundmaterials der Zellwandfolien - Oberflächenhypothese - massgebend beeinflusst wird.
(n∗=0) des Glasgrundmaterials der Zellwandfolien - Oberflächenhypothese - massgebend beeinflusst wird.
Für die Spannungsanalysen, die die Grundlage der Prognosen der mechanischen Verhaltensweisen des Modellpolyederschaumglases "ORTHO" bildeten, wurden nur die Verhältnisse 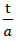 = f (ρ,ε) bei jeweils konstant gehaltenem Parameter ε variiert.
= f (ρ,ε) bei jeweils konstant gehaltenem Parameter ε variiert.
Die Zugfestigkeit, der Elastizitätsmodul und die Querdehnungszahl der als Kontinuum betrachteten Zellwandfolien aus Vollglas wurden gemäss Abschnitt Nr. 1.3.1 zu
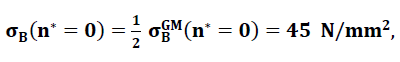
E(n∗=0)=72′600 N / mm2 und
ν (n∗=0)=0.21 angenommen!
Die Kerbwirkungen an den Stellen, wo sich je drei Zellwandfolien schneiden, wurden für die Bestimmung der Bruchfestigkeiten vernachlässigt.
In der Tabelle auf Seite 91 wurden die Ergebnisse der so ermittelten Druck und Zugfestigkeiten (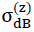 ,
,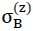 ) zusammengestellt und in Bild Nr. 45 graphisch dargestellt.
) zusammengestellt und in Bild Nr. 45 graphisch dargestellt.
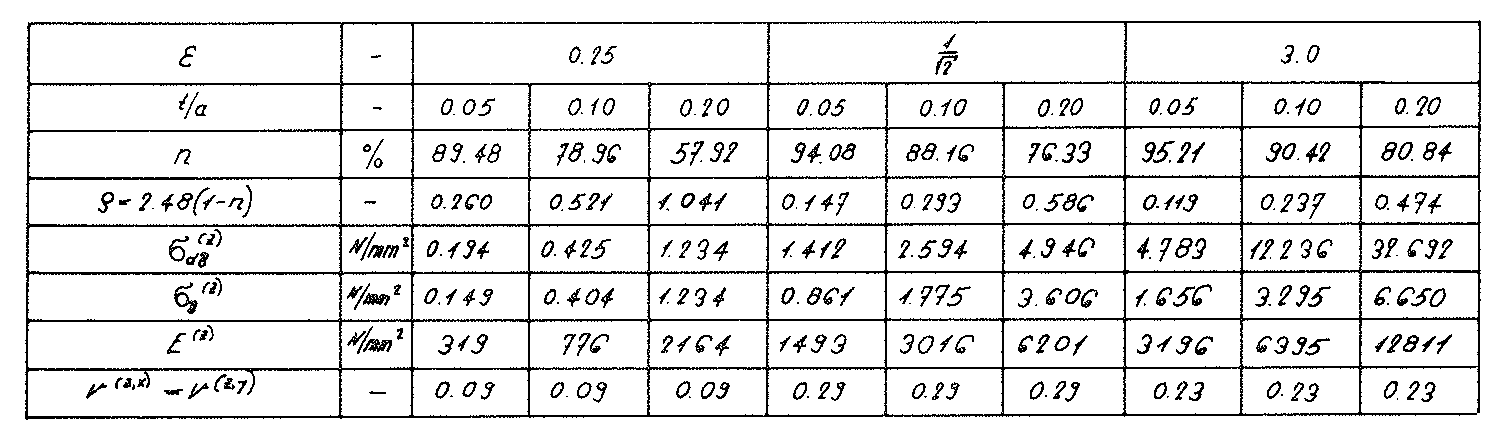
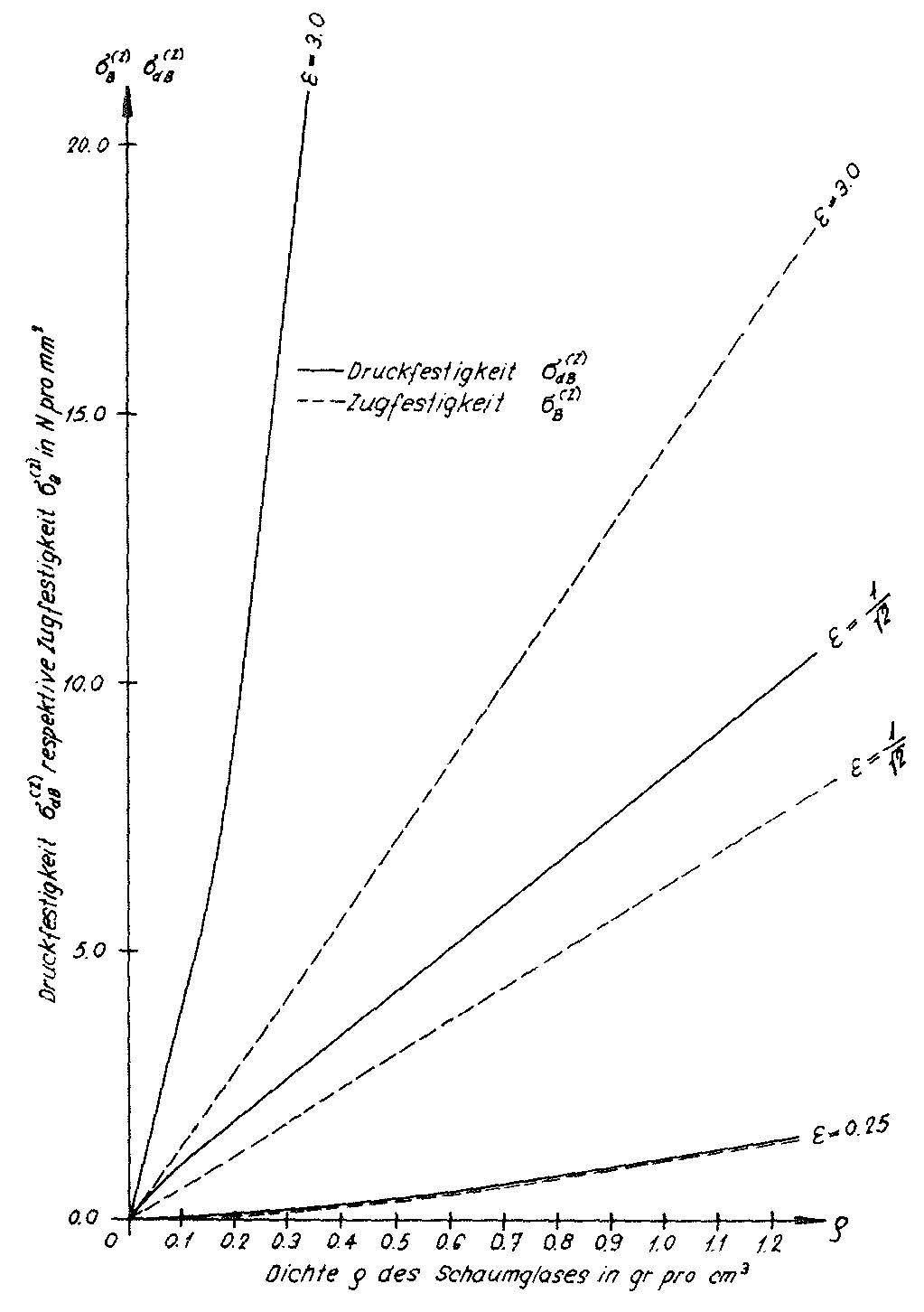
Bild Nr. 45. Die Bruchfestigkeit des Modellschaumglases "ORTHO"
Da das Modellpolyederschaumglas "ORTHO" eine homogene Anisotropie aufweist, gilt bezüglich seiner Elastizität dieselbe Theorie wie für das Modell "TOP" in Abschnitt Nr. 1.3.2. Das bedeutet, dass auch im Bezugssystem x1,x2,x3auf Bild Nr. 43 der Zusammenhang zwischen dem Spannungsvektor 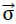 und dem Verzerrungsvektor
und dem Verzerrungsvektor 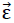 durch die Beziehung
durch die Beziehung
80)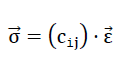
ausgedrückt werden kann 1).
Wie bereits gesagt, bilden die Symmetrieelemente des Modellschaumglases "ORTHO" die Punktgruppe (Kristallklasse) 4 / mmm. Somit weist die symmetrische Matrix (cij) der Elastizitätsmoduln cij nach dem Neumann'schen Prinzip (siehe Abschnitt Nr. 1.3.2.2.4.) folgende Struktur auf:
81)
Trotz der Tatsache, dass die Elastizität des Modellschaumglases "ORTHO" nur durch die sechs Elastizitätsmoduln c11,c12,c13,c33,c44 und c66 genau beschrieben werden kann, wurden für unsere groben Abschätzungen nur die unter der äusseren Belastung σ(z)=−σ3 auftretenden Grössen
82)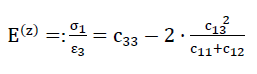
83)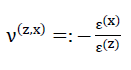 und
und
84)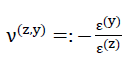
rechnerisch bestimmt.
- 1)Die Vektoren
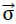 und
und 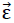 wurden in Abschnitt Nr. 1.3.2.2.4. definiert.
wurden in Abschnitt Nr. 1.3.2.2.4. definiert.
Dabei gelten folgende Gleichheiten:
- 1)σ3=−σ(z) ;
- 2)ε3=ε(z) ;
- 3)ε(x)=ε(y)=ε1=ε2 , und
- 4)ν(z,x)=ν(z,y).
In den folgenden Ausführungen sollen die Werte E(z) und ν(z,x)=ν(z,y) als Elastizitätsmodul beziehungsweise als Querdehnungszahl des Modellschaumglases bezeichnet werden!
In der Tabelle auf Seite 91 wurden auch die simultan mit den Bruchfestigkeiten an der verstärkten Materiellen Subeinheit bestimmten Werte E(z) und ν(z,x)=ν(z,y) eingetragen. Bild Nr. 46 zeigt die Graphen E(z)(ρ,ε) und ν(z,x)(ρ,ε)=ν(z,y)(ρ,ε) für die drei Parameter ε=0.25; 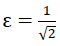 und ε=3.0.
und ε=3.0.
Die Diagramme in den Bildern Nr. 45 und Nr. 46 lehren, dass die Bruchfestigkeiten 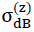 und
und 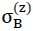 sowie die Elastizitätsmoduln E(z) des Modellschaumglases "ORTHO" bei gleichbleibender Dichte ρ mit steigendem Wert des Parameters ε sehr stark anwachsen. Diese Erkenntnis kann natürlich auch auf reale stark orthotrope Polyederschaumgläser in angepasster Art und Weise übertragen werden.
sowie die Elastizitätsmoduln E(z) des Modellschaumglases "ORTHO" bei gleichbleibender Dichte ρ mit steigendem Wert des Parameters ε sehr stark anwachsen. Diese Erkenntnis kann natürlich auch auf reale stark orthotrope Polyederschaumgläser in angepasster Art und Weise übertragen werden.
Das Beispiel des Modelles "ORTHO" weist darauf hin, dass bei Druckbelastung - analog wie bei den handelsüblichen Isolierbacksteinen - Schaumglasbausteine mit länglichen polyedrischen in Richtung der Druckspannungstrajektorien ausgerichteten Poren optimale Trageigenschaften zeigen werden.
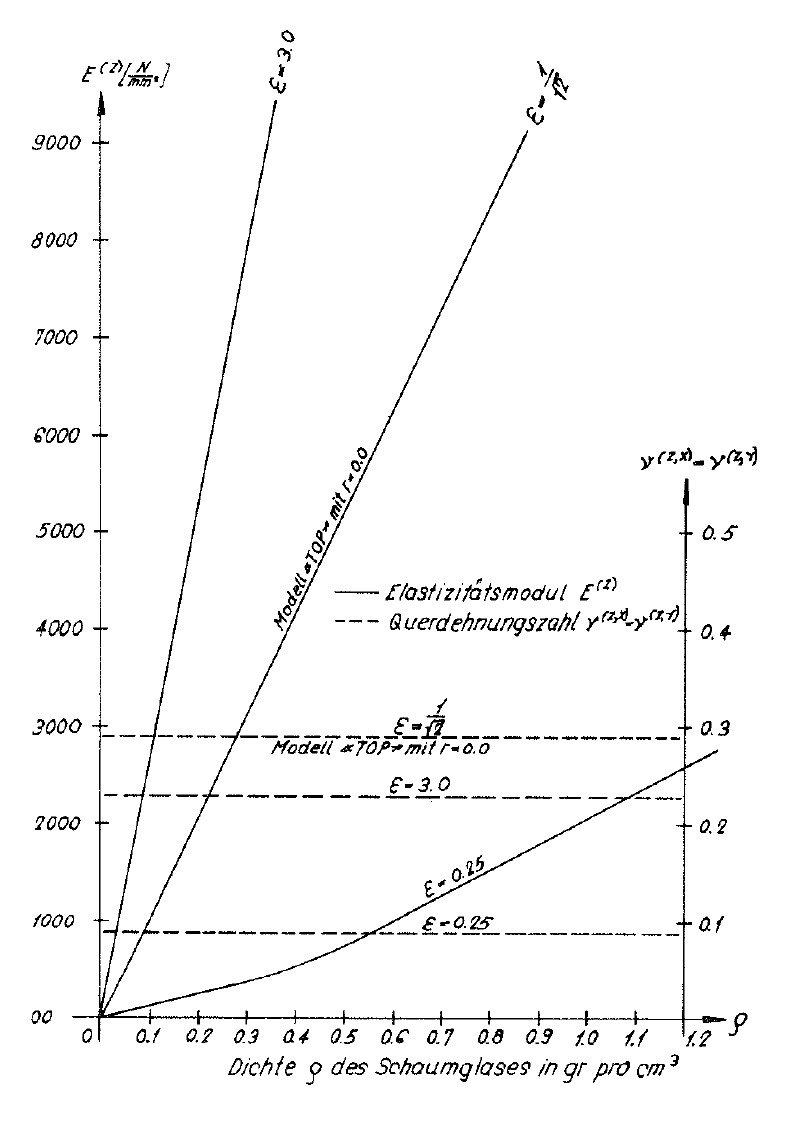
Bild Nr. 46. Elastizitätsmodul und Querdehnungszahl des Modellschaumglases "ORTHO"